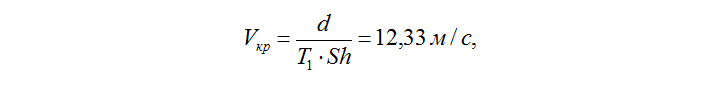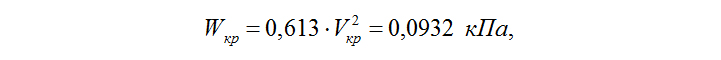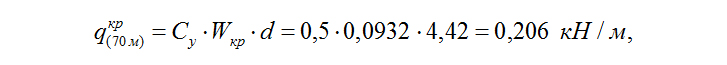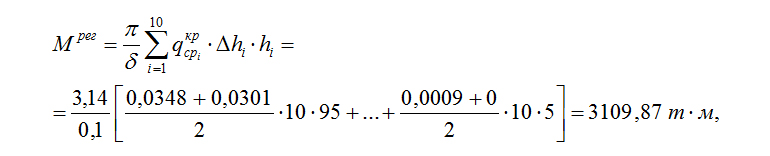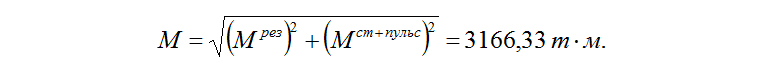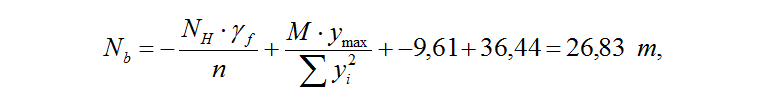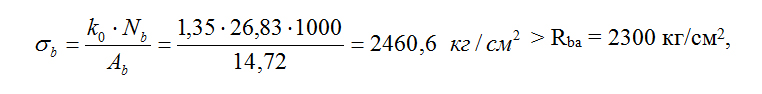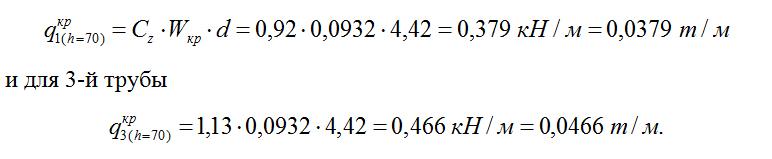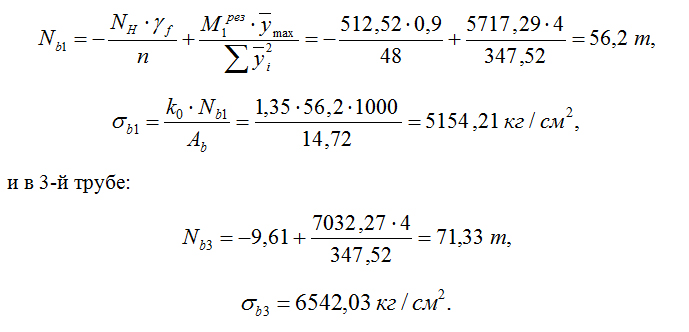ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ ПО УСТАНОВЛЕНИЮ ПРИЧИН РАЗРЫВА АНКЕРНЫХ БОЛТОВ И ОБРАЗОВАНИЯ ТРЕЩИН В ЧЕТЫРЕХ РЯДОМ СТОЯЩИХ СТАЛЬНЫХ ДЫМОВЫХ ТРУБАХ

Сущев Сергей Петрович – Генеральный директор Центра исследований
экстремальных ситуаций, доктор технических наук, профессор

Адаменко Иван Арсентьевич – Главный инженер директор Центра исследований
экстремальных ситуаций, кандидат технических наук, доцент

Самарин Виталий Викторович – Ведущий специалист Центра исследований
экстремальных ситуаций, доктор технических наук, профессор

Суслонов Александр Аркадьевич – Начальник отдела Центра исследований
экстремальных ситуаций, кандидат технических наук

Калугин Владимир Тимофеевич – Профессор кафедры баллистики
и аэродинамики Московского государственного технического
университета им. Н.Э. Баумана, доктор технических наук профессор

Киндяков Евгений Борисович – Инженер-конструктор ОАО «ОКБ Сухого»

 

---

После возведения в 2004 году четырех стальных дымовых труб высотой 100 м каждая с ребрами жесткости и интерцепторами (рис.1) оказалось, что они испытывают повышенные вибрации и колебания. В связи с этим в 2007 году трубы были обследованы представителями организации, которая выполняла проектирование этих труб. В заключении по результатам обследования был сделан вывод о том, что трубы не имеют дефектов и повреждений, снижающих их несущую способность, находятся в работоспособном состоянии и следующее обследование рекомендуется выполнить в 2011 году.

Однако летом 2008 года, т.е. через год после обследования, было обнаружено, что 14 анкерных болтов на трех трубах разорваны (рис.2) и в горизонтальных сварных швах появились сквозные трещины (рис.3), которые при колебаниях труб то открываются, то закрываются.

При этом характерно то, что разрывы анкерных болтов и трещины, как правило, расположены в направлении поперек оси, на которой расположены трубы.

Поверочный расчет одной из труб как отдельно стоящей (без учета всех остальных труб) на действие собственного веса, крена фундамента и ветровой нагрузки (сумма статической и пульсационной составляющих), выполненный на основании СНиП 2.01.03-85 «Сооружение промышленных предприятий» [1] и СНиП 2.01.07-85* «Нагрузки и воздействия» [2], показал, что напряжения во всех анкерных болтах в основном металле и сварных швах трубы не превышают расчетных сопротивлений сталей, используемых при их изготовлении.

В связи с тем, что результаты выполненного расчета не учитывают поперечных колебаний трубы и не объясняют наблюдаемых в натуре разрывов анкерных болтов и трещин в сварных швах трубы, размеры которой удовлетворяют условию H/d > 10 (см. п.6.1 [1]), дополнительно был выполнен поверочный расчет на вихревое возбуждение (ветровой резонанс) отдельно стоящей трубы; здесь H = 100 м – высота сооружения, d = 4,02 м – минимальный размер поперечного сечения, расположенного на уровне 2/3 H. При этом, как указано в работе [3], никаких ссылок на методику, согласно которой следует производить поверочный расчет на ветровой резонанс, данный СНиП не предоставляет. Поэтому для оценки возможности возникновения ветрового резонанса в отдельно стоящей трубе воспользуемся формулами, приведенными в [4, 5].

Критическая скорость ветра, вызывающая резонансные колебания сооружения в направлении, перпендикулярном ветровому потоку, определяется по формуле

где   Т₁ = 2,39 с (f₁ = 0,418 Гц) – период собственных колебаний трубы по 1-й форме;

Sh = 0,15 – число Струхаля для сечений с угловыми точками;

d = 4,42 м – диаметр сооружения на уровне 2/3H ≈ 70 м.

Полученная критическая скорость удовлетворяет условию 5 м/с ≤ V_кр = 12,33 м/с ≤ 25 м/с [7], что является еще одним условием необходимости проведения расчета на ветровой резонанс.

Скоростной напор, соответствующий критической скорости:

и амплитуда расчетной динамической силы (горизонтальная поперечная распределенная нагрузка) на высоте ≈ 70 м составляет

где   С_у = 0,5 – коэффициент поперечной силы для цилиндрических сооружений с поперечными сечениями, имеющими угловые точки.

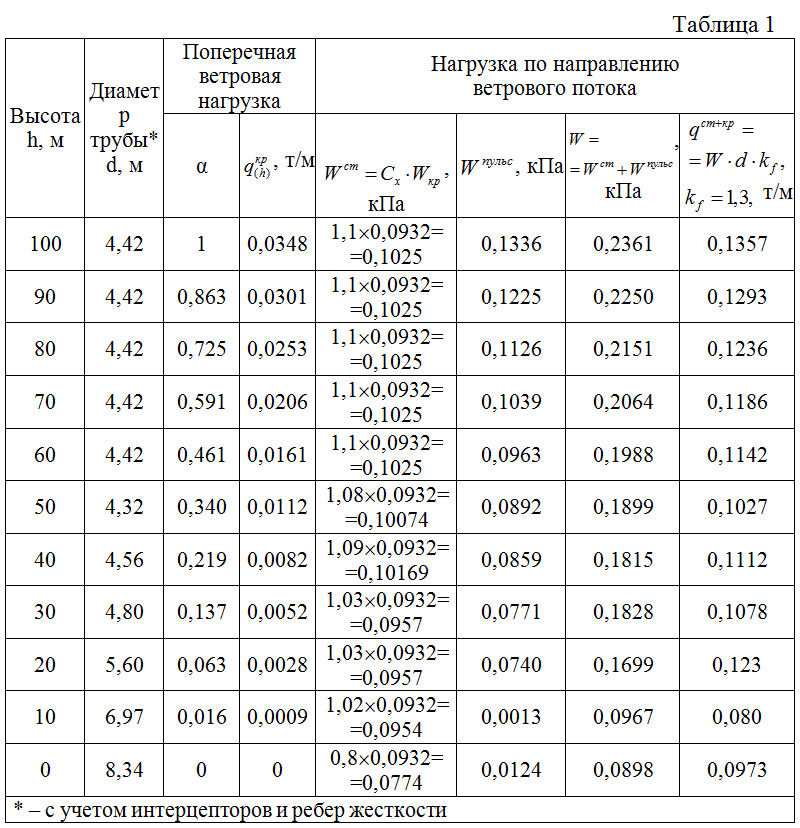
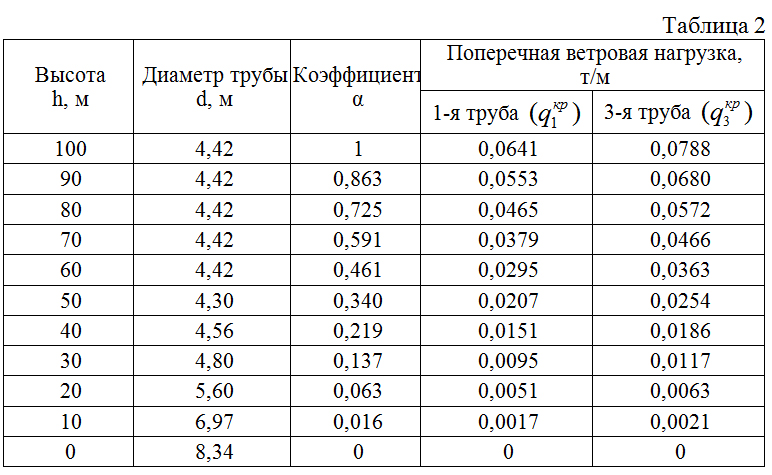
Расчетные горизонтальные поперечные распределенные нагрузки на других отметках q^кр_(h) пропорциональны ординатам 1-й формы колебаний (α) и представлены в табл.1. В этой же таблице приведены средние (статические) и пульсационные составляющие, полная ветровая нагрузка, а также расчетные горизонтальные распределенные нагрузки по направлению ветрового потока при V = V_кр = 12,33 м/с.

Изгибающий момент в основании трубы поперек ветрового потока (при резонансе):

 

где   δ = 0,1 – логарифмический декремент затухания колебаний для мачт и стальных футерованных дымовых труб.

Изгибающий момент в основании трубы по направлению действия ветра:

Суммарный изгибающий момент в основании трубы

Растягивающее усилие в крайнем анкерном болте при ветровом резонансе:

где   N_H – 512,52 т – нормативное нормальное усилие в основании трубы (вес трубы);

γ_f = 0,9 – коэффициент надежности по нагрузке;

y_max = 4 м – расстояние от центра трубы до крайнего анкерного болта;

Σy_i² = 347,52 м² – сумма квадратов расстояний от каждого анкера до диаметральной линии трубы.

Напряжение в этом анкерном болте

где   k₀ = 1,35 – коэффициент условия работы;

А_b = 14,72 см² – площадь сечения анкера Ø48 мм;

R_ba = 2300 кг/см² – расчетное сопротивление анкерных болтов, выполненных из стали 09Г2С [6].

Таким образом, расчет на ветровой резонанс отдельно стоящей трубы с поперечным коэффициентом аэродинамики С_y = 0,5 показал, что напряжения в крайних анкерных болтах незначительно превышают расчетное сопротивление стали 09Г2С, из которой они выполнены, что не может быть причиной такого массового выхода из строя анкеров, наблюдаемого в натуре. Кроме того, поверочный расчет по 1-му предельному состоянию стального ствола трубы на полученную нагрузку при резонансе показал, что напряжения в элементах трубы (в царгах, ребрах жесткости и в сварных швах) по всей высоте трубы не превышают расчетного сопротивления стали 255, из которой они изготовлены.

Так что же все-таки является причиной повышенных вибраций (колебаний) всех четырех труб, разрыва анкерных болтов и образования сквозных трещин в трубах?

Для ответа на этот вопрос предлагается выполнить расчет, в котором продольный и поперечный аэродинамические коэффициенты определяются с помощью более сложной расчетной схемы. Вместо отдельно стоящей трубы предлагается рассмотреть пространственную близкую к натуре систему, в которой четыре трубы расположены в ряд вдоль вблизи стоящего здания (см.рис.1).

Такая расчетная схема позволяет при действии ветра выявить структуру вихревых потоков и их влияние на динамические нагрузки, действующие на неподвижно стоящие трубы, т.е. определить продольные и поперечные аэродинамические коэффициенты для каждой трубы. Расчет дозвукового обтекания дымовых труб выполняется методом контрольного объема (МКО) [10]. Метод основан на использовании осредненных по Рейнольдсу уравнений Навье-Стокса, замкнутых моделью турбулентности. Расчетная область разбивается на конечное число контрольных объемов. В центре каждого контрольного объема или на его грани располагается узел расчетной сетки, в котором и производится определение параметров течения. Принимается, что скорость изменения во времени какой-либо физической величины в контрольном объеме равна скорости изменения во времени этой же величины в контрольном объеме плюс полный поток этой величины через поверхности контрольного объема. В этом случае осредненные по Рейнольдсу уравнения Навье-Стокса могут быть записаны в виде 

Граничные условия задаются следующим образом. На границе счетной области «вход» параметры течения считаются известными. На границе «выход» ставится условие открытой области («Opening»), а на обтекаемой поверхности – условие непротекания. Итерации по пространству проводятся с помощью явной схемы второго порядка точности.

Для выбора модели турбулентности и проверки достоверности получаемых в численном эксперименте результатов были проведены тестовые расчеты, в которых использовались различные однопараметрические и двухпараметрические модели турбулентности. Расчеты осуществлялись с помощью комплекса вычислительных программ Fluent (свидетельство NLA 18-03-03). По результатам тестовых расчетов была выбрана SST – модель турбулентности. В дальнейшем весь численный эксперимент был проведен с использованием данной модели турбулентности и указанного выше комплекса вычислительных программ.

Прежде чем проводить численный эксперимент с использованием МКО по сложной схеме с четырьмя трубами и экранирующим зданием, по той же программе был проведен расчет аэродинамических характеристик и параметров обтекания изолированной (отдельно стоящей) трубы. Были рассмотрены два варианта: гладкая труба (без ребер жесткости) и труба такого же диаметра, но с ребрами жесткости (РЖ) как в реальной трубе. Интерцепторы, установленные на высоте от 60 до 100 м, решено было не учитывать, так как, во-первых, в реальных трубах их ширина (20 см) оказалась в 2-3 раза меньше той, которая рекомендуется в справочной литературе [7], и, во-вторых, принято считать, что интерцепторы гасят колебания, которые в настоящей работе как раз и являются одним из объектов исследования.

В результате расчетов на ЭВМ получены структура обтекания и соответствующие линии тока (рис.4 и 5) для двух видов труб при скорости ветра V = 25 м/с, которая примерно соответствует нормативному значению ветрового давления в районе расположения комбината (W₀ = 30 кг/м²) [2].

На этих рисунках видно, что за ребрами жесткости и за гладкой цилиндрической частью труб образуется зона отрывного течения. Вихревой след за гладкой трубой (рис.5) меньше, чем вихревая пелена за трубой с ребрами жесткости (рис.4), особенно в приземной части. Сравнительные аэродинамические характеристики труб представлены на рис.6. Величина продольной (по направлению ветрового потока) силы Х трубы с ребрами жесткости (С_х = 0,63) больше, чем трубы без ребер жесткости (С_х = 0,52). Порядок абсолютной величины поперечной (боковой) силы Z обеих труб примерно одинаковый (С_z = 0,19÷0,23).

В аэродинамических характеристиках трубы с РЖ, хотя и прослеживается колебательный характер поперечной силы Z с частотой ν = 0,54 Гц, но эти колебания представляют собой систему знакопостоянных циклов с небольшой амплитудой, что не может быть причиной существенных колебаний труб, которые наблюдаются в натуре. В гладкой трубе, в отличие от трубы с РЖ, четко выраженных колебаний силы Z не наблюдается.

Выполненный численный расчет показал, что поперечный аэродинамический коэффициент отдельно стоящей трубы с РЖ (С_z = 0,23) более чем в 2 раза меньше коэффициента C_y = 0,5, который был принят выше при расчете на ветровой резонанс. Следовательно, при С_z = 0,23 напряжения в анкерных болтах и в материале трубы при расчете по той же методике [5] не превышают расчетных сопротивлений сталей, из которых они выполнены.

Таким образом, выполненные выше исследования показали, что в одиночной трубе, имеющей ребра жесткости, как при расчете по СНиП [1, 2], в том числе и на ветровую нагрузку, так и при проверке на ветровой резонанс по методике [5] и с помощью численного метода контрольных объемов не выявлено причин, которые могли бы вызвать разрывы анкерных болтов и появление трещин в самой трубе и ее ребрах жесткости. Полученные с помощью МКО аэродинамические характеристики одиночной трубы с ребрами жесткости не дают объяснений наблюдаемым в натуре вибрациям и колебаниям труб.

В связи с этим следующим этапом в исследованиях является численный эксперимент с использованием сложной расчетной схемы, которая описана выше и включает 4 трубы и экранирующее здание.

В этих расчетах использовалась ортогональная система координат, в которой ось O_x направлена вдоль линии расположения труб, а ось O_y – вверх, вдоль вертикальной оси трубы. Нумерация труб проводилась по направлению набегающего потока, в качестве газодинамических параметров которого были выбраны осредненные значения по высоте: V_∞ = 25 м/с, T_∞ = 293 К, P_∞ = 101325 Па, угол скольжения β = 10° [8].

Из-за ограничения памяти используемого компьютера высота Н труб была принята равной 30 м. Диаметр царг составляет 4,02 м, двенадцать ребер жесткости, расположенные по всей высоте переменной ширины от 45,0 см вверху до 216 см в основании труб, точно соответствуют натуре так же, как и расстояние между осями труб – 21,11 м и расстояния от здания до оси расположения труб – 8 м.

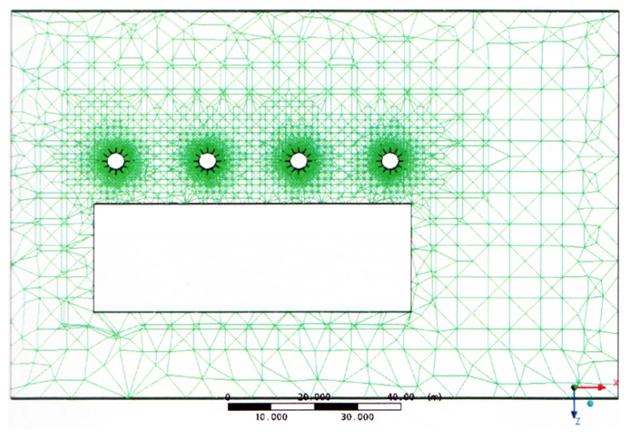
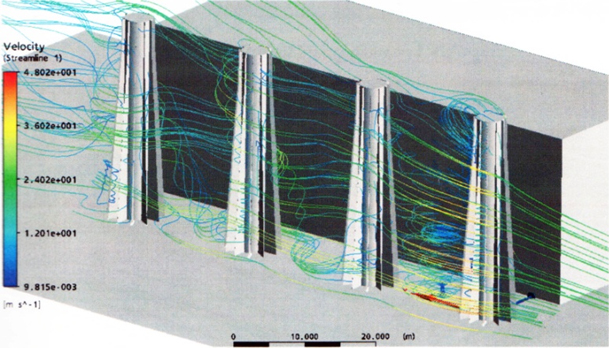
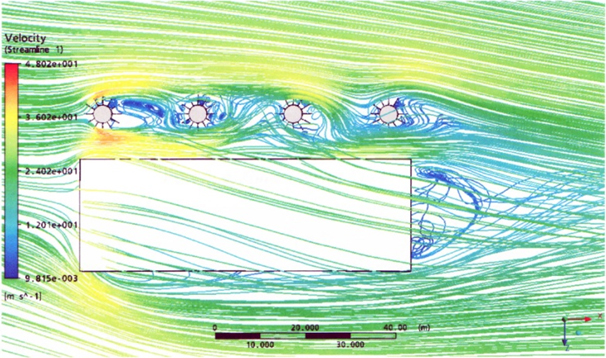
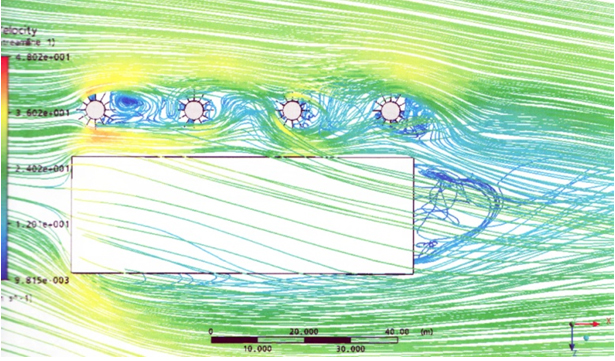
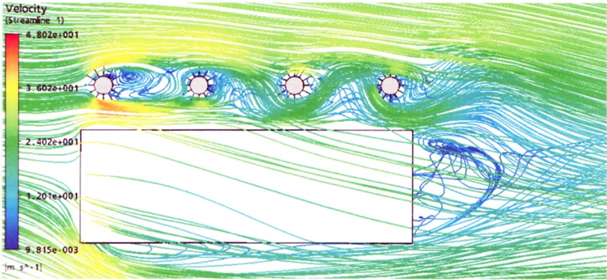
Пространственная расчетная сетка была построена в виде тетраэдров и составила 5 588 043 расчетных элементов (ячеек). Вид горизонтальной проекции расчетной сетки в сечении на высоте h = 15 м показан на рис. 7. Расчет производился в диапазоне времени от 0 до 10 с с шагом интегрирования Δt = 0,01 с. Структура обтекания комбинации 4 трубы + здание (рис.8) показывает, что в областях между ребрами жесткости образуются мощные вихревые жгуты, поднимающиеся вертикально вверх и сходящие вниз по потоку, образуя вихревую пелену за трубой. Вихрь, сходящий с первой трубы, воздействует на вторую трубу, стоящую за ней. В свою очередь, вихри, срывающиеся с поверхности второй трубы, ударяют по третьей и так далее. Кроме того, находящееся рядом здание оказывает экранирующий эффект, изменяя характер обтекания труб и направление линий тока, которые изменяются во времени и для нескольких моментов представлены на рис. 9-11.

 

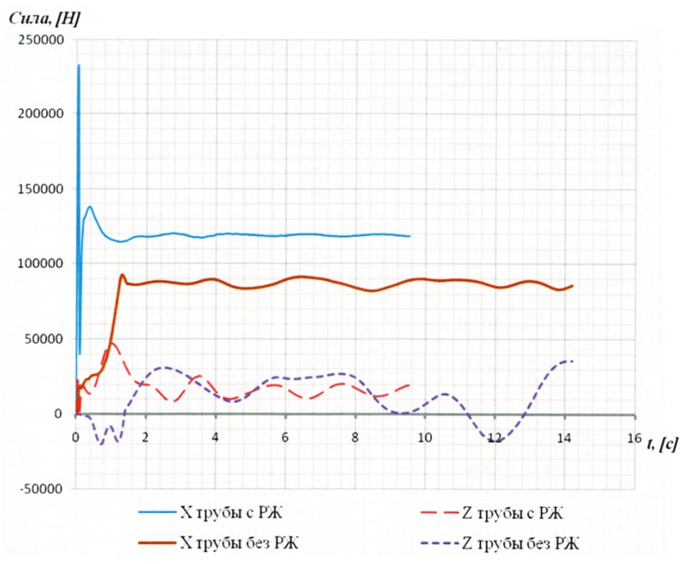
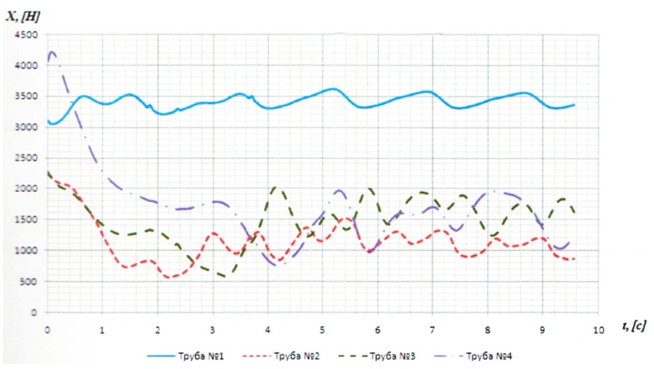
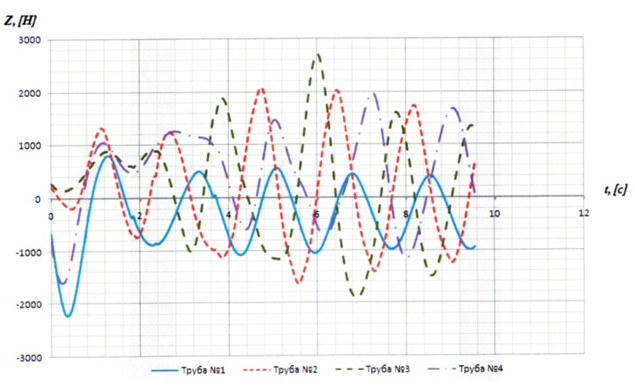
Кроме того, в результате расчетов получены аэродинамические характеристики (АДХ) труб, а именно: изменение во времени продольных (по оси O_x, рис.12) и поперечных (по оси O_z, рис.13) сил, действующих на 1 погонный метр высоты каждой трубы. Из графиков видно, что полученный характер обтекания вызывает импульсную нагрузку, частота ν = 1/T которой приблизительно равна 0,58; 0,45; 0,54 и 0,53 Гц для труб №1, 2, 3 и 4 соответственно. Однако характер колебаний в продольном (по оси O_x) и в поперечном (по оси O_z) направлениях существенно отличается. Если в продольном направлении колебания происходят в режиме знакопостоянных циклов с относительно небольшой амплитудой (см.рис.12), то в поперечном направлении колебания представляют собой знакопеременные циклы (почти симметричные) с достаточно большими амплитудами (см.рис.13). Это приводит к сильной раскачке труб в поперечном направлении, а учитывая, что полученные частоты близки к собственной частоте трубы и что скорость ветра в потоке принималась равной V = 25 м/с > V_кр = 12,33 м/с, то в данном случае имеем дело с интерференсным галопированием [8].

Если при вихревом возбуждении интенсивные колебания возникают в строго определенном интервале скоростей (в нашем случае приблизительно при V_кр = 12,33 м/с), то галопирование происходит при всех скоростях ветра выше критических.

При этом трубы при галопированиии испытывают не только поперечные колебания, но и вертикальные, что и наблюдается в натуре на всех трубах, в одних меньше, в других больше, практически постоянно при ветреной погоде.

Для определения аэродинамических коэффициентов из полученных графиков АДХ выбирается максимальная (абсолютная) амплитуда удельной аэродинамической силы, действующей на каждую трубу и, зная удельную силу ветрового давления в подходящем ветровом потоке, путем деления первой на вторую получаем значения продольных (С_х) и поперечных (С_z) аэродинамических коэффициентов для каждой трубы: 1-я труба (С_х = 1,48 и С_z = 0,92); 2-я труба (С_х = 0,62 и С_z = 0,88); 3-я труба (С_х = 0,82 и С_y = 1,13) и 4-я труба (С_х = 0,8 и С_z = 0,8).

Анализ полученных аэродинамических коэффициентов показывает, что принятая расчетная схема в виде четырех рядом стоящих стальных дымовых труб с ребрами жесткости и экранирующего здания при действии ветрового потока, направленного под углом β = 10° к оси расположения труб, приводит к следующим результатам. Например, во 2-й и 3-й трубах поперечные коэффициенты (С_z) больше, чем продольные (С_х), а в 4-й трубе эти коэффициенты равны С_х = 0,8. Кроме того, оказалось, что наибольшие поперечные коэффициенты имеют 1-я и 3-я трубы, а минимальный поперечный коэффициент С_z = 0,8 для 4-й трубы больше, чем поперечный коэффициент С_y = 0,5, который использовался при расчете на ветровой резонанс одиночной трубы по методике справочника [5]. Зная новые аэродинамические поперечные коэффициенты и используя ту же методику, выполним расчет на резонанс и определим напряжения в анкерных болтах 1-й и 3-й труб. При этом амплитуда расчетной динамической силы (горизонтальная поперечная распределенная нагрузка) на высоте h = 70 м для 1-й трубы

Расчетные горизонтальные поперечные нагрузки на других отметках пропорциональны ординатам 1-й формы собственных колебаний (α) трубы и представлены в табл.2.

Изгибающий момент в основании 1-й и 3-й труб поперек ветрового потока соответственно равен

Растягивающее усилие и напряжение в «крайнем» анкерном болте при ветровом резонансе в 1-й трубе:

Полученные растягивающие напряжения в «крайних» анкерных болтах в 1-й и 3-й трубах не только в 2,2÷2,8 раза больше расчетного сопротивления R_ba = 2300 кг/см² стали 09Г2С [6], но и превышают предел текучести (4400 кг/см²), а для 3-й трубы – и временное сопротивление разрыву (5950 кг/см²).

Растягивающее напряжение в «крайних» анкерных болтах во 2-й трубе s_b2 = 4930 кг/см² и в 4-й трубе (s_b4 = 4482 кг/см² также превышает предел текучести.

Таким образом, выполненный расчет по определению аэродинамических коэффициентов по сложной схеме с использованием МКО показывает, что при ветровом резонансе в всех четырех трубах возможен разрыв анкерных болтов. При обследовании труб на месте разрывы анкерных болтов были обнаружены в трех трубах.

Согласно [1], стальные дымовые трубы при критических скоростях ветра, вызывающих резонансные колебания сооружения, следует рассчитывать на усталость в соответствии с требованиями [9]. Проверке подлежат стыковые швы оболочки (ребер жесткости) дымовых труб, при этом в расчете должно учитываться не менее 2 млн. циклов напряжения. Расчет на выносливость (усталость) следует производить по формуле [9]

если допустить, что напряжения пропорциональны действующим поперечным силам, то, используя рис.13, определяем ρ:

для 1-й трубы – ρ₁ = -0,47 и = 1,269;

для 3-й трубы – ρ₃ = -0,666 и = 1,154.

Следовательно, максимальные напряжения в швах при расчете на выносливость (усталость) должны удовлетворять условию:

Анализ полученных результатов показывает, что в 1-й трубе усталостных трещин в швах оболочки при резонансе не будет; можно ожидать образование трещин в швах ребер жесткости на высоте от 20 до 25 м, где (s_max > 1302 кг/см² (в табл.3 выделено жирным курсивом).

В 3-й трубе по расчетам можно ожидать образование усталостных трещин в швах оболочки трубы на высотках от 20 до 30 м и от 50 до 60 м (в табл.3 выделено красным), а трещин в швах ребер жесткости на высотах от 0 до 35 м, где (s_max > 1184 кг/см² (в табл.3 выделено жирным курсивом).

Аналогичные расчеты, выполненные для 2-й (s₂^max ≤1174 кг/см²) трубы, показали, что в ней можно ожидать появление усталостных трещин только в швах ребер жесткости на высотах от 17,5 до 25 м. В 4-й трубе расчет на выносливость при резонансе не выявил образование трещин в швах ни в оболочке ни в ребрах жесткости, т.к. по всей высоте трубы s₄^max < 1283 кг/см². Теоретически выполненный прогноз по образованию усталостных трещин в швах оболочек и ребер жесткости четырех рядом стоящих стальных дымовых труб для некоторых из них достаточно точно соответствует трещинам, которые были обнаружены на месте при детальном обследовании труб.

 

Выводы

 

1. Для определения продольных и поперечных аэродинамических коэффициентов на основе метода контрольных объемов смоделирована задача обтекания четырех стоящих в один ряд дымовых стальных труб с ребрами жесткости около экранирующего здания.
2. С помощью полученных аэродинамических поперечных коэффициентов вычислены усилия и напряжения в анкерных болтах и усталостные напряжения в швах оболочек всех труб и их ребрах жесткости при ветровом резонансе. Результаты теоретических расчетов позволили установить, что причиной разрыва анкерных болтов и образования трещин в системе дымовых стальных труб, обнаруженных на реальном объекте при его обследовании, являются колебания, вызванные вихревым возбуждением.
3. Причиной наблюдаемых в натуре вибраций и колебаний труб является интерференсное галопирование. Если при вихревом возбуждении интенсивные колебания возникают в определенных интервалах скоростей ветра, то галопирование происходит при всех скоростях выше критических, а так как в районе, где расположен комбинат, практически постоянно дуют сильные ветра, то такие вибрации и колебания труб практически никогда не прекращаются.

 

Библиографический список

 

1. СНиП 2.09.03-85. Сооружения промышленных предприятий. Госстрой СССР. – М.: ЦИТП Госстроя СССР, 1990. 56 с.
2. СНиП 2.01.07-85*. Нагрузки и воздействия. – М.: ОАО «ЦПП», 2008. 44 с.
3. Никитин П.Н., Оносов Г.В. Опыт проектирования дымовых труб // Пром. и гражд. стр-во. 2009. №5. С. 24-27.
4. Руководство по расчету зданий и сооружений на действие ветра. – М.: Стройиздат, 1978. 216 с.
5. Динамический расчет сооружений на специальные воздействия: Справочник проектировщика / М.Ф. Барштейн, Н.М. Бородочев. Л.Х. Блюмина и др.; Под ред. Б.Г. Коренева, И.М. Рабиновича. – М.: Стройиздат, 1981. 215 с.
6. СП 53-102-2004. Общие правила проектирования стальных конструкций/Госстрой России. – М.: ЦНИИСК им. Кучеренко, 2004. 131 с.
7. Дужих Ф.П., Осоловский В.П., Ладыгичев М.Г. Промышленные дымовые и вентиляционные трубы. Справочное издание / Под ред. Ф.П. Дужих. – М.: Теплотехник, 2004. 464 с.
8. Нагрузки и воздействия на здания и сооружения / В.Н. Гордеев, А.И. Лантух-Лященко, В.А. Пашинский, А.В. Перельмутер, С.Ф. Пичугин; Под ред. А.В. Перельмутера. – М.: Издательство Ассоциации строительных вузов, 2008. 482 с.
9. СНиП II-23-12*. Стальные конструкции. – М.: ОАО «ЦПП», 2008. 90 с.
10. Чернышев Д.Д., Холонов И.С., Атаманчук А.В. Исследование обтекания пакета трех труб ветровым потоком с помощью метода контрольных объемов // Пром. и гражд. стр-во. 2009. №11. С.40-42.