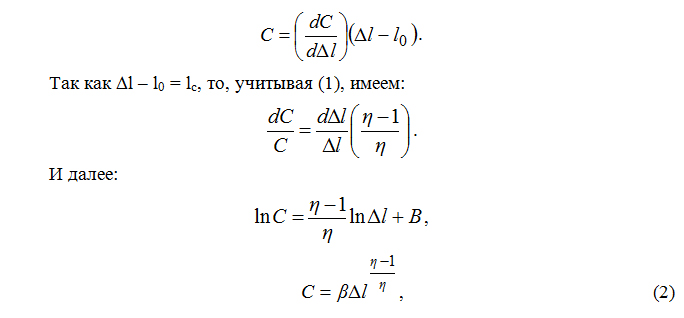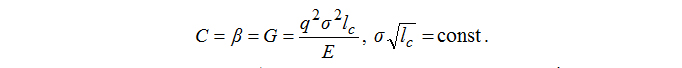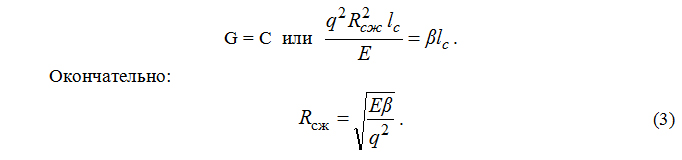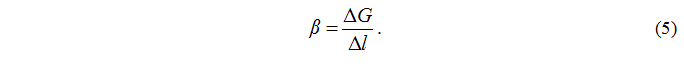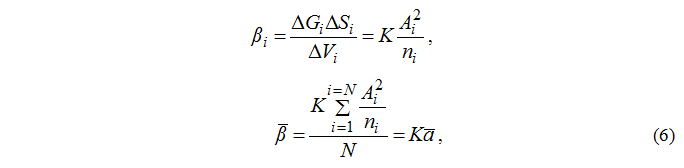ИССЛЕДОВАНИЕ ПРОЧНОСТИ БЕТОНА НА СЖАТИЕ И ВОЗМОЖНОСТИ ЕЁ КОНТРОЛЯ МЕТОДОМ ТЕРМОАКУСТИЧЕСКОЙ ЭМИССИИ

Горбунов И.А. – Профессор кафедры «Испытания сооружений»
Московского государственного строительного университета,
кандидат технических наук

Васильков В.Э. – Старший научный сотрудник
кафедры «Испытания сооружений» Московского государственного
строительного университета

---

Назначение прочностных характеристик бетона в расчётах конструкций по предельным состояниям базируется на результатах разрушающих испытаний на сжатие стандартных кубов с ребром 15 см. Целью исследования является установление универсальных параметров неразрушающего контроля, связанных с кубиковой прочностью R_куб. бетона любой структуры.

На кафедре «Испытания сооружений» МГСУ разработан метод оценки прочности бетона с использованием параметров термоакустической эмиссии (ТАЭ) [1]. Ограниченность практического использования метода объясняется отсутствием серийных приборов для регистрации параметров ТАЭ и оборудования для создания локального нагрева. На опытных установках получена универсальная градуировочная зависимость «кубиковая прочность тяжёлого бетона – параметр ТАЭ». Вместе с тем отмечается, что характер зависимости меняется при изменении амплитудно-частотных характеристик приборов и пьезопреобразователя (ППР), расположения ППР относительно зоны нагрева, геометрии нагреваемого участка поверхности. В силу этих причин следует рассмотреть вопрос о принципиальной обоснованности предлагаемой методики контроля прочности бетона.

1. Особенности деструкции бетона при сжатии и локальном термонагружении

Стабильный характер процесса трещинообразования наблюдается как при сжатии, так и в условиях термонагружения. При этом, во многих исследованиях отмечается, что при сжатии образуются микротрещины, которые обеспечивают развитие трещин. В ранних работах, посвященных этому вопросу, усматривается стремление авторов провести границы, разделяющие эти стадии. Метод АЭ позволил получить данные, указывающие на условность нижней и верхней границ трещинообразования. Микротрещинообразование начинается с первых этапов нагружения материала и не прекращается вплоть до разрушения. Интересной особенностью, отмечаемой при сжатии бетонных образцов, является относительное увеличение доли высокоамплитудных импульсов в амплитудном распределении сигналов АЭ для более прочного бетона. При этом возрастают и сами амплитуды сигналов АЭ. Однако, в испытаниях на сжатие особенности трещинообразования по данным АЭ носят качественный характер. Различные удалённость и ориентация трещин – источников АЭ относительно ППР, а также затухание импульса на его пути к ППР, определяемое привнесённой сжатием деструкцией бетона, существенно влияют на амплитуды регистрируемых сигналов АЭ.

В методе ТАЭ реализуется схема стабильного роста трещин в локальных объёмах бетона, «подготовленных» микротрещинообразованием. При нагреве или охлаждении участка поверхности создаётся напряжённое состояние, сравнимое с полем вторичных напряжений при сжатии. В обоих случаях отсутствуют напряжения на боковых гранях. Регистрация образующихся при трещинообразовании сигналов ТАЭ происходит в условиях минимальных искажений в амплитудах принятого импульса при температурном воздействии на участке поверхности бетона в форме узкого полукольца с размещением ППР в центре соответствующей окружности.

2. Аналитическая модель разрушения бетона при сжатии

 Как отмечалось выше, основной особенностью деструкции бетона является стабильный рост трещин при увеличении сжимающих напряжений. В механике разрушения рассматривается случай стабильного роста трещины при увеличении растягивающих напряжений, ориентированных перпендикулярно к направлению распространения трещины [2]. Для бетона описание деструкции с позиции механики разрушения требует допущения, что одноосное сжатие создаёт внутреннее сложнонапряжённое состояние, в котором структурные растягивающие напряжения однозначно связаны с внешними напряжениями сжатия. Объективно оценивая условность такого предположения, тем не менее введём его, сославшись на аналогию использования в механике разрушения коэффициентов напряжённого состояния при определении коэффициентов интенсивности напряжений К₁, К₂, К₃ в устье трещины. Таким образом, предположим, что вторичные растягивающие напряжения σ_р определяются соотношением::

σ_р = qσ_сж.

Условием стабильного роста трещины является равенство интенсивности выделения упругой энергии G и энергетического сопротивления разрушению материала C при увеличении длины трещины на величину Dl [2]. Переход к неустойчивому развитию трещины (рис. 1) наступает в случае:

l_c = (Δl – l₀) – критическая длина трещины;
l₀ – начальная длина трещины;
E – модуль упругости материала.

Для определения зависимости С = f(Dl) принимается допущение [2]:

l_c = –ηl₀.                                                     (1)

Согласно рис.1, имеем дифференциальное уравнение при различных начальных длинах трещины l₀ и соответствующих точках касания:

 

где    B = lnβ;
β – энергетическая постоянная сопротивления разрушению материала.

Анализ выражения (2) при η = 1 (начальная длина трещины является критической) приводит к классическому решению механики разрушения хрупкого тела:

При одноосном сжатии бетона критическая длина трещины l_c значительно превышает начальную l₀. Из формулы (2) имеем:

h >> 1;    C ≡ β l.

В этом случае допущение (1) не является жёстким ограничением, а понятие критической длины трещины теряет свой смысл, так как на определённом предельном уровне напряжений при их бесконечно малом приращении G – прямая и С – прямая пересекаются в бесконечности. Расчётное для предельных напряжений выражение принимает вид:

Решение, парадоксальное с позиции механики разрушения, не является столь уж неожиданным для объёмных сжимаемых бетонных конструкций, в которых большие трещины не являются редкостью. При рассмотрении прочности образца куба в рамках представленной модели зависимость (3) принципиально не меняется. Ограничение критической длины трещины размерами образца, а также поперечное стеснение на нагружаемых гранях учитываются заменой коэффициента q² на γ:

средние значения R̃_куб, Е̃, β̃. Однако, учитывая вероятностный характер параметров выражения (4), представляется практически целесообразным проведение регрессионного анализа результатов эксперимента, в котором широкий диапазон изменения прочности достигается вариацией структуры бетона. В этом исследовании основной методической задачей является нахождение способа оценки параметра b, физический смысл которого, исходя из вышеизложенного, просматривается достаточно определённо.средние значения R̃_куб, Е̃, β̃. Однако, учитывая вероятностный характер параметров выражения (4), представляется практически целесообразным проведение регрессионного анализа результатов эксперимента, в котором широкий диапазон изменения прочности достигается вариацией структуры бетона. В этом исследовании основной методической задачей является нахождение способа оценки параметра b, физический смысл которого, исходя из вышеизложенного, просматривается достаточно определённо. средние значения R̃_куб, Е̃, β̃. Однако, учитывая вероятностный характер параметров выражения (4), представляется практически целесообразным проведение регрессионного анализа результатов эксперимента, в котором широкий диапазон изменения прочности достигается вариацией структуры бетона. В этом исследовании основной методической задачей является нахождение способа оценки параметра b, физический смысл которого, исходя из вышеизложенного, просматривается достаточно определённо.

редние значения R̃_куб, Е̃, β̃. Однако, учитывая вероятностный характер параметров выражения (4), представляется практически целесообразным проведение регрессионного анализа результатов эксперимента, в котором широкий диапазон изменения прочности достигается вариацией структуры бетона. В этом исследовании основной методической задачей является нахождение способа оценки параметра b, физический смысл которого, исходя из вышеизложенного, просматривается достаточно определённо.

3. Анализ возможности использования метода ТАЭ для определения b-энергетической характеристики сопротивления бетона разрушению при сжатии

Условием стабильного роста трещины является равенство значений функции энергетического сопротивления и интенсивности освобождаемой упругой энергии, которая в свою очередь тесно связана с энергией акустических сигналов, регистрируемых методом АЭ. В связи с тем, что при силовом сжатии и термонагружении создаются условия стабильного роста трещин, в случае термодеструкции функция энергетического сопротивления разрушению бетона сохраняет свой вид:

C = β l или ΔC = β Δl = ΔG.

При этом параметр β соответствует конкретной кубиковой прочности бетона и определяется из выражения:

Из формулы (5) следует, что размерность b – [Нм/м³]. Учитывая степень свободы ориентации трещин вокруг оси нагружения при сжатии, можно рассматривать b как величину выделившейся упругой энергии, отнесённой к объёму ΔV, в котором прорастает трещина на длину Δl. Если допустить, что скачкообразно освобождаемая упругая энергия пропорциональна квадрату максимальной амплитуды механической волны, а объём, в котором прорастает трещина, линейно связан с числом микротрещин, в нём образовавшихся, то среднюю величину β̃ можно получить по информации ТАЭ, то есть в результате локального температурного воздействия на поверхности куба перед его испытанием на сжатие:

при

где    N – суммарное число импульсов от преобразованных высокоамплитудных механических волн;
A_i – приведённое в соответствии с номером канала анализатора импульсов значение сигнала от высокоамплитудной механической волны на i-м этапе прорастания трещины на длину Δl_i;
n_i – число импульсов от микротрещин по данным о низкоамплитудных механических волнах в интервале между i-м и (i–1)-м этапами прорастания трещины;
ΔG_i – интенсивность освобождаемой упругой энергии на единицу площади увеличившихся берегов трещины;

v – скорость прохождения ультразвука;
r – плотность бетона по результатам взвешивания образцов, а при натурных обследованиях – по данным неразрушающих испытаний;
Σn – сумма импульсов от низкоамплитудных механических волн, зарегистрированных за контролируемый период термонагружения;
A – значение каждого из импульсов от высокоамплитудных механических волн.

Записав формулу (8) в виде

получим базовое выражение для проведения 3-факторного эксперимента, представляющего собой комплексные неразрушающие испытания образцов-кубов бетона с последующими механическими разрушающими испытаниями по определению прочности на сжатие. В результате статистической обработки может быть получена единая градуировочная зависимость. Проведённые экспериментальные исследования показали, что, учитывая взаимную корреляцию факторов, а также высокую значимость параметра α̃, достаточно надёжной может оказаться упрощённая оценка прочности бетона на сжатие только по одной косвенной характеристике b^*.

Параметр b^* определяется по результатам испытаний методом ТАЭ и отличается от β̃ по формуле (7) тем, что коэффициент K не рассматривается как постоянная величина, а является функцией, корректирующей логические построения (2)-(7) предлагаемой аналитической модели. Функция от параметров ТАЭ (К – поправка) улучшает статистические характеристики градуировочной зависимости «R_куб – β̃». 

Библиографический список 

1. Положительное решение патентной экспертизы по заявке №5005872/28 от 08.07.92 г.
2. Броек Д. Основы механики разрушения. – М.: Высш. шк. 1980. – С.109-116.