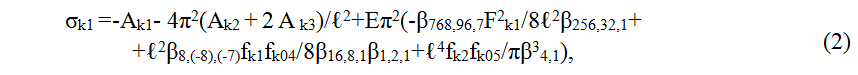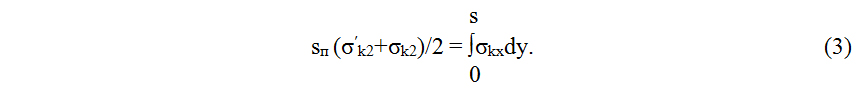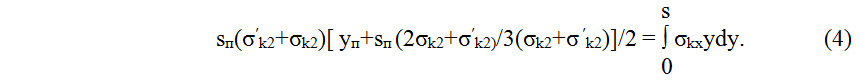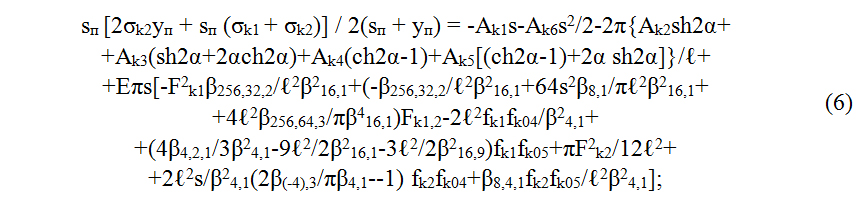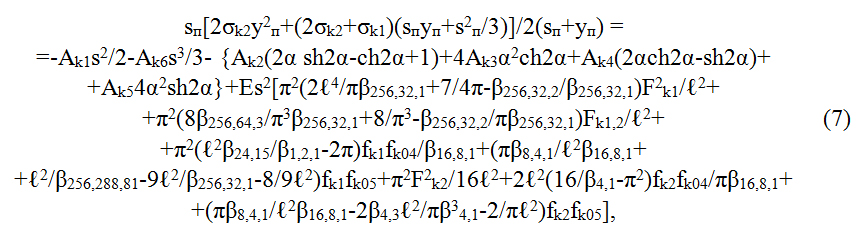Ильяшенко А.В. – Доцент кафедры «Строительная механика»
Московского государственного строительного университета,
кандидат технических наук
Исследование несущей способности сжатых упругих тонкостенных стержней, имеющих начальную погибь и претерпевших местную потерю устойчивости, связано с определением редуцированного поперечного сечения стержня. Основные положения, принятые для исследования напряжённо-деформированного состояния в закритической стадии сжатых неидеальных тонкостенных стержней, приведены в работах [1-3]. В данной статье рассматривается закритическое поведение стержней, которые представляются в виде совокупности совместно работающих элементов – пластинок с начальной погибью, имитирующих работу полок уголковых, тавровых и крестообразных профилей. Это так называемые полки-пластинки с одним упруго защемлённым краем и другим свободным (см.рисунок). В работах [1-2] такая пластинка относится к типу II.
Было установлено [3], что разрушающая нагрузка, характеризующая несущую способность стержня, значительно превышает нагрузку Ркр(м), при которой происходит местная потеря устойчивости несовершенного профиля. Из графиков, представленных в [3], видно, что деформации продольных волокон по периметру поперечного сечения в закритической стадии становятся крайне неодинаковыми. В волокнах, удалённых от рёбер, деформации сжатия при увеличении нагрузки уменьшаются, а при нагрузках, близких к предельным, из-за резкого искривления этих волокон вследствие начальных погибей и всё возрастающих стрелок продольных полуволн, образовавшихся после местной потери устойчивости, появляются и интенсивно растут деформации растяжения.
Участки поперечного сечения с искривлёнными продольными волокнами сбрасывают напряжения, как бы выключаются из работы стержня, ослабляя эффективное сечение и уменьшая его жёсткость. Итак, несущая способность тонкостенного профиля не ограничивается местной потерей устойчивости. Полная нагрузка, воспринимаемая более жёсткими (менее искривлёнными) участками поперечного сечения, может значительно превосходить величину Ркр(м).
Получим эффективное, редуцированное сечение, исключив неработающие участки профиля. Для этого используем выражение для функции напряжений Фk(х,у), описывающей напряжённое состояние k-ой пластинки типа II (см. [1]).
Перейдём к закритическим напряжениям σkх (в направлении действия внешней сжимающей силы), определяемым в наиболее неблагоприятном сечении стержня (х=0). Запишем их в общем виде:
σkx=∂2Фk(Akm,y, fkj, fkoj, βc,d, βc,d,j,ℓ, s) ∕ ∂ y2, (1)
где постоянные интегрирования Аkm (m=1,2,…,6) и стрелки составляющих приобретённых прогибов fkj(j=1,2) определяются из решения системы разрешающих уравнений [2]. Эта система уравнений включает в себя нелинейные вариационные уравнения и граничные условия, описывающие совместную работу неидеальных пластинок профиля. Стрелки fkoj (j=1,2,…,5) составляющих начального прогиба k-й пластинки определяются для каждого типа профиля экспериментально;
ℓ – длина образующейся при местной потере устойчивости полуволны [2];
s – ширина пластинки;
βc,d=cs2 + dℓ2;
βc,d,j= cs4 + dℓ2s2 + gℓ4;
c, d, j – целые положительные числа.
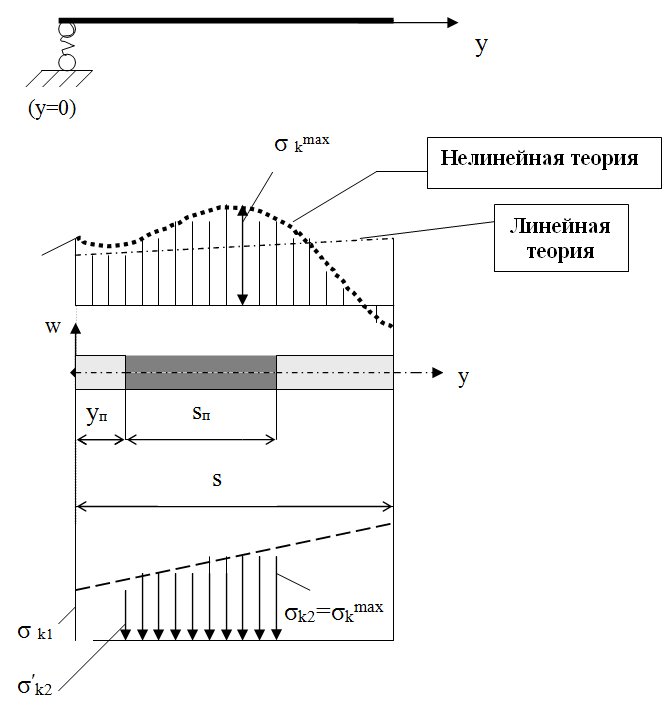
Приведённую или эффективную ширину редуцированного сечения пластинки-полки (типа II) обозначим через sп. Для её определения выпишем условия перехода от действительного поперечного сечения стержня к редуцированному:
1. Напряжения в продольных волокнах у начальной грани пластинки (при у=0), примыкающей к ребру (см.рисунок), остаются такими же, как и полученные по нелинейной теории (1):
где F2kr=f2kr+2fk0rfkr.
Для определения напряжения σk2=σkmax необходимо подставить в (1) ординату наиболее загруженного продольного волокна, которая находится из условия: ∂σkx/∂y=0.
2. Сумма внутренних усилий в пластинке при переходе к редуцированному сечению в направлении действия сжимающей силы не меняется:
3. Момент внутренних усилий относительно оси, проходящей через начальную грань (у=0) перпендикулярно плоскости пластинки, остаётся прежним:
Из рисунка очевидно, что
σ′k2 = σk1 + yп(σk2-σk1) / (yп + sп). (5)
Запишем систему уравнений для определения приведённой ширины пластинки sп. Для этого подставим (1) и (5) в (3) и (4):
где α=πs/ℓ ; Fkr,ξ=fkrfkoξ+fkrfkξ+fkorfkξ;
r, ξ – целые положительные числа.
Полученная система уравнений (6) и (7) даёт возможность определить приведённую ширину sп каждой из пластинок-полок, составляющих сжатый претерпевший местную потерю устойчивости тонкостенный стержень. Таким образом, действительное поперечное сечение профиля заменили на редуцированное.
Далее по общей теории тонкостенных стержней – теории В.З.Власова, – можно определить критическую нагрузку, вызывающую общую потерю устойчивости полученного стержня с изменённым эффективным сечением.
Предлагаемая методика представляется полезной как в теоретическом, так и в практическом плане при расчётах на несущую способность сжатых предварительно искривлённых тонкостенных стержней, в которых по эксплуатационным требованиям допустимо местное волнообразование.
Библиографический список
- Ильяшенко А.В., Ефимов И.Б. Напряжённо-деформированное состояние после местной потери устойчивости сжатых тонкостенных стержней с учётом начальной погиби // Строительные конструкции и материалы. Защита от коррозии. – Уфа: Тр.ин-та НИИпромстрой, 1981. – С.110-119.
- Ильяшенко А.В. К расчёту тонкостенных тавровых, уголковых и крестообразных профилей с начальной погибью // Свайные фундаменты. – Уфа: Сб. науч. тр. Ниипромстроя, 1983. – С. 110-122.
- Ильяшенко А.В., Ефимов И.Б. Экспериментальное исследование тонкостенных стежней с искривлёнными пластинчатыми элементами // Организация и производство строительных работ. – М.: Центр.Бюро н.-т. информации Минпромстроя, 1983.