Колесов А.И. Нижегородский государственный
архитектурно-строительный университет
Ямбаев И.А. Нижегородский государственный
архитектурно-строительный университет
Морозов Д.А. Нижегородский государственный
архитектурно-строительный университет
Современные требования к экономичному, но надежному проектированию зданий и сооружений, эффективно используя резервы несущей способности их элементов, требует выполнения дополнительных научных исследований для выявления и оценки действительного напряженно-деформированного состояния (НДС) конструкций. Особенно это актуально для сжато-изгибаемых и внецентренно-сжатых стержней.
Применение сжато-изогнутых и внецентренно-сжатых элементов в строительных конструкциях широко распространено в связи с поисками наиболее экономичных и эффективных решений при новом проектировании, а также при совершенствовании конструктивных схем, зданий и сооружений на этапах проектирования и монтажа при реконструкции зданий или при усилении отдельных конструкций.
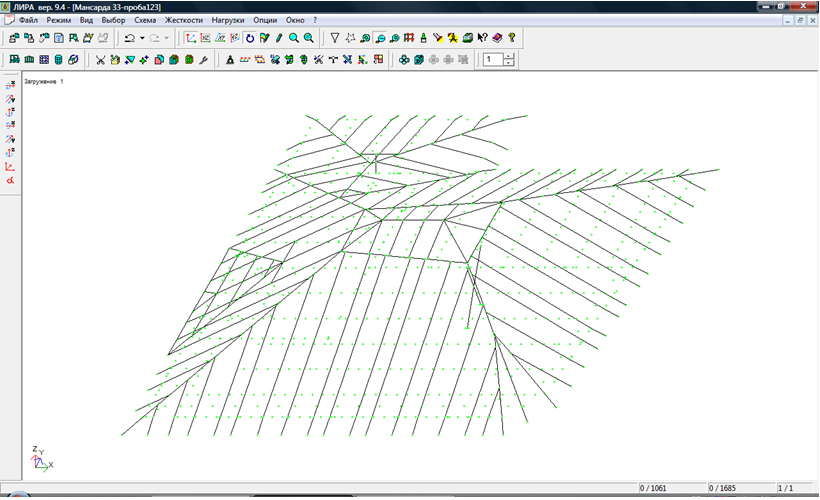
На рис. 1 представлена расчетная схема элементов мансарды ООО «Центр Серна» (ул. Б.Печерская, г. Н.Новгород), запроектированная специалистами кафедры металлических конструкций ННГАСУ. Все элементы данной конструкции являются сжато-изогнутыми и выполнены из тонкостенных профилей повышенной жесткости (ППЖ). Отдельные элементы конструкции мансарды обладают относительно небольшой гибкостью, но пониженной, как показывают исследования (см. ниже), несущей способностью.
На рис. 2 представлены повреждения в форме погибей нижнего и верхнего поясов фермы мартеновского цеха ОАО «ВМЗ» (г.Выкса). Данные погиби приводят к появлению значительных эксцентриситетов в конструкции, к внецентренному растяжению и внецентренному сжатию конструктивных элементов.

Рис. 2. Общая погибь элемента из плоскости фермы со стрелой погиби f = 500 мм (мартеновский цех ОАО «ВМЗ», г. Выкса)
Учитывая широкое распространение сжато-изогнутых и внецентренно-сжатых элементов в конструкциях, проблема исследования их надежности и действительного НДС является актуальной как с точки зрения экономии материала, так и для повышения их долговечности.
Инженерная методика проектирования и расчета сжато-изогнутых элементов сложилась в конце 19 – начале 20 веков. Научные работы, связанные с расчетом сжато-изгибаемых стержней, были опубликованы Эйлером, Т.Карманом, Рошем и Бруннером, Вестергором и Осгудом, Хвалла, Ежеком, Юнгом, Ф. Блейхом, Н.С. Стрелецким, А.В. Геммерлингом, Пинаджаном, Н.И. Климовым, Энгессером и Ясинским, Тетмайером и Консидером, В.З. Власовым и С.П. Тимошенко, В.В. Горевым, Г.И. Белым.
В 1908 году Т. Карман [1] обратил внимание на чувствительность коротких стержней и стержней средней длины даже к незначительным эксцентриситетам приложенных нагрузок, что заметно уменьшает несущую способность сжатых стержней.
Энгессер [5, 6] предложил формулу определения критической силы в упруго-пластической области. Этот вопрос позднее был уточнен Ясинским [7-10].
В 1926 году Рош и Бруннер [2, 3] опубликовали упрощенную теорию устойчивости внецентренно-сжатых стержней и на основе ряда опытов доказали правильность полученных ими теоретических результатов.
Тимошенко С.П. [11-15] разработал общие положения энергетической теории потери устойчивости сжато-изогнутого стержня.
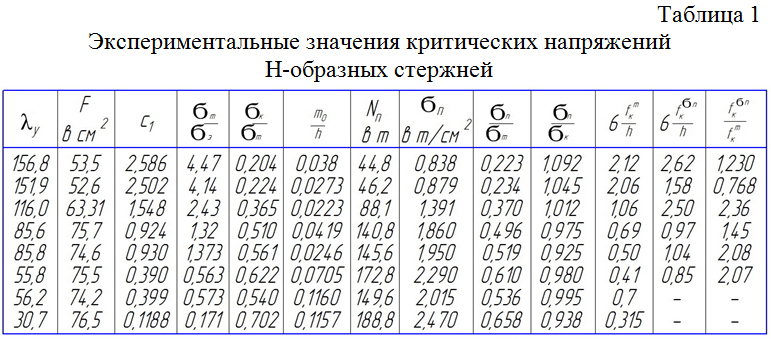
В 1952 году в ЦНИПСе под руководством Н.И. Климова [4] были проведены испытания на внецентренное сжатие восьми стальных двутавровых стержней, результаты которых приведены в табл.1. Геммерлинг сравнил с результатами теоретического расчета и получил некоторые расхождения.
Исчерпание несущей способности большинства сжатых (с учетом начальных искривлений или случайных эксцентриситетов, принятых в соответствии с допускаемыми отклонениями, установленными в нормах на изготовление стальных конструкций [16]) и сжато-изгибаемых элементов происходит из-за потери устойчивости формы, которая определяется, главным образом, параметрами расчетной длины и жесткости сечения, а также пояснением неучтенных расчетами пластических деформаций в сечениях элементов.
Основные резервы нормативной методики расчета сжато-изогнутых стержней, на наш взгляд, следующие:
— современные нормативные методики расчета сжато-изогнутых элементов применяют значительные ограничения работы в упругопластической стадии при различных гибкостях стержней;
— расчетные таблицы нормативных методик получены для прямоугольных сечений с переходом на другие сечения через коэффициент формы;
— коэффициенты формы сечения не полностью учитывают различные случаи потери устойчивости и несущей способности. Так анализ коэффициентов влияния формы сечения показал [17], что такой подход к решению задач может как занижать (до 7% и выше), так и повышать (до 10% и выше) несущую способность стержней;
— несовершенства в определении расчетных длин в плоскости и из плоскости действия изгибающих моментов.
Ниже представлены численные и натурные исследования сжато-изогнутых стержней. Численно в ППП MSC «NASNRAN» был выполнен расчет 20 моделей прокатных двутавров №10; 20; 30; 40 длиной 6 м с жесткими заделками по концам стержня на 5 сочетаний сжимающей силы N и изгибающего момента M; 20 моделей прокатных двутавров №10; 20; 30; 40 длиной 3 м с граничными условиями в виде шарниров на 5 сочетаний сжимающей силы N и изгибающего момента M; и 30 моделей профилей повышенной жесткости ПН-100-0,8 гибкостью 20; 40; 60; 80; 100; 120 также на 5 сочетаний сжимающей силы N и изгибающего момента M.
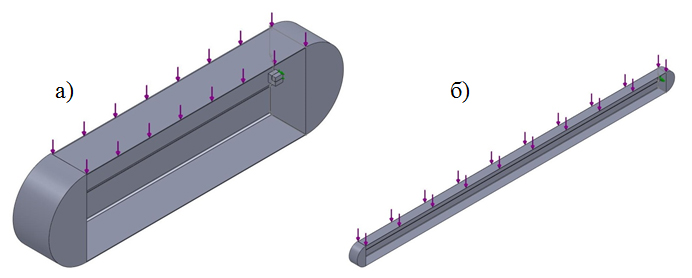
Рис. 3. Схемы конечно-элементных моделей профилей повышенной жесткости ПН-100-0,8: а – гибкостью 20; б – гибкостью 120
Для конечно-элементных моделей ППЖ на обоих концах расчетной модели стержня установлены цилиндры (см. рис.3), предназначенные для снятия концентрации напряжений в точках закрепления и приложения нагрузки. Точки закрепления стержня расположены на оси, проходящей через центр тяжести сечения. С одного конца стержень закреплен от перемещения во всех направлениях, а с другого конца закреплен только от перемещений, перпендикулярных оси стержня, к которой так же прикладывается сжимающая нагрузка. Таким образом обеспечиваются граничные условия в виде подвижных и неподвижных шарниров.
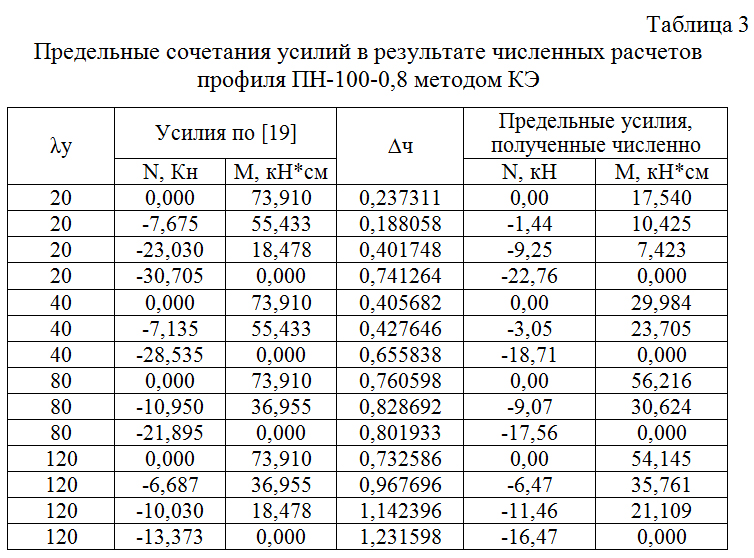
Варианты усилий, рассчитанных по нормам и полученных численно и их предельные соотношения, указаны в табл.2 и 3.
В результате численного расчета прокатных двутавров выявлены запасы несущей способности по сравнению с существующей инженерной методикой расчета по [18] (до 30%) при различных соотношениях N и M и разных гибкостях.
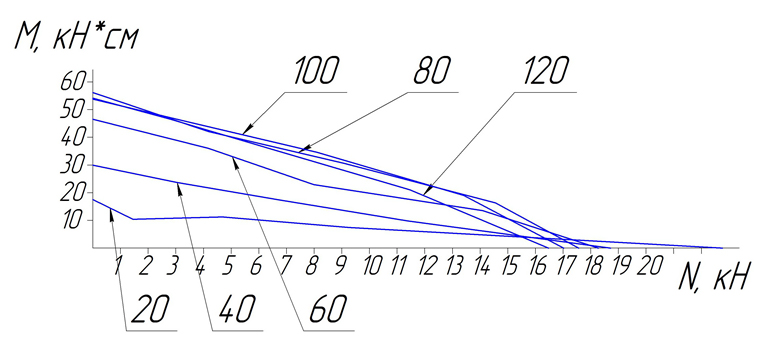
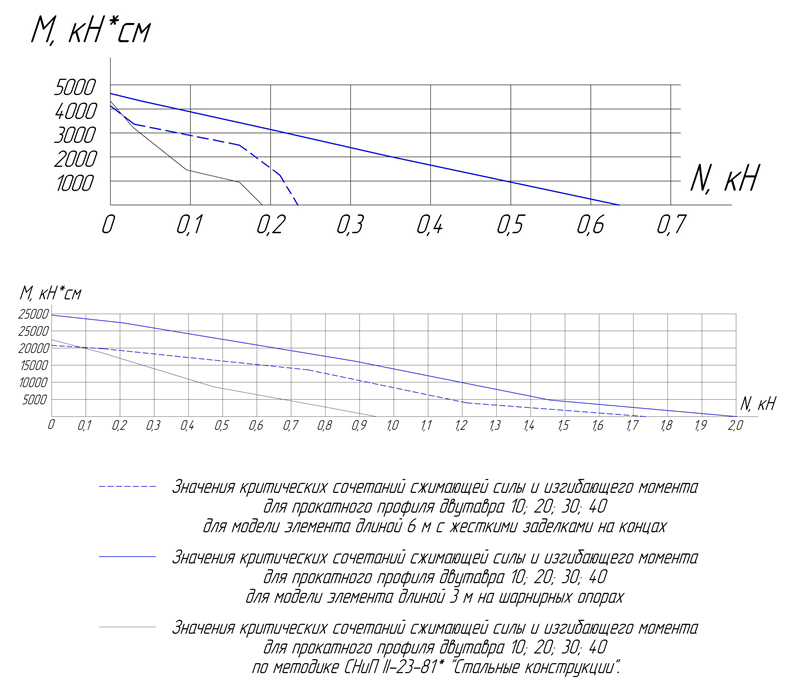
В результате численных расчетов получено напряженно-деформированное состояние рассматриваемых стержней и построены графики значений критических сочетаний N и M для различных гибкостей (рис. 4, 5).
Исчерпание несущей способности тонкостенного профиля повышенной жесткости ПН-100-0,8 происходит либо в форме потери общей устойчивости из плоскости действия момента, либо вследствие одновременной потери общей устойчивости из плоскости действия момента и потери местной устойчивости полок на опоре в зависимости от соотношений N и M при разных гибкостях.
Здесь ∆ч – коэффициент отношения численных значений, полученных методом конечных элементов, к значениям по [19].
При численном расчете тонкостенных ППЖ получен недобор несущей способности при малых и средних гибкостях (до 20% и более) по сравнению с расчетом по рекомендациям Э.Л. Айрумяна [19] без учета коэффициента условий работы γс.

Рис. 6. Общая картина приведенных напряжений по Мизесу и деформаций сжато-изгибаемого элемента длиной 500 мм, сечением ПН-100-0,8
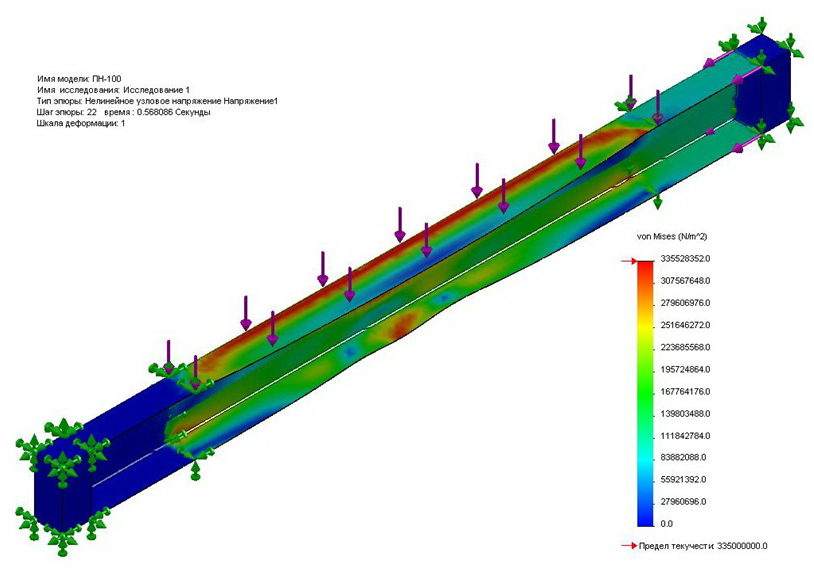
Рис. 7. Общая картина приведенных напряжений по Мизесу и деформаций сжато-изгибаемого элемента длиной 800 мм, сечением ПН-100-0,8
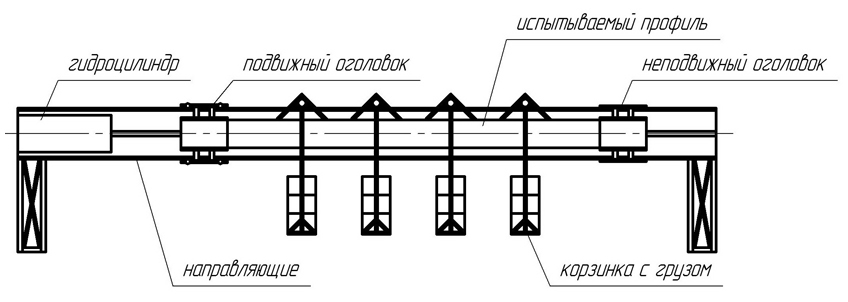
Разработана лабораторная установка для испытаний сжато-изгибаемых элементов (рис.8, 9). Она представляет собой две направляющие на стойках, к которым жестко крепятся два башмака, в которые вставляется стержень ППЖ, но один башмак имеет степень свободы, т.е. может перемещаться вдоль стержня за счет специальной тележки. Образец одновременно загружается поперечной распределенной нагрузкой от установленных сверху корзинок с грузами и продольной сжимающей силой от гидроцилиндра.
Установка состоит из испытуемого образца, двух швеллеров, двух оголовков, горизонтального гидроцилиндра, соединенного с оголовком, и установочных ножек. Посредством регулировочных винтов оголовков обеспечены горизонтальность и соосность профиля и гидроцилиндра. Соединение между оголовком и профилем выполнено на винтах. Установка является наименее трудоемкой и металлоемкой, а также позволяет нагружать стержень из ППЖ малыми ступенями (от 1 кН).
В центральной лаборатории ННГАСУ были проведены испытания на сжатие с изгибом стержней из ППЖ ПН-100-0,8. Схема каждого испытываемого образца представляет собой тонкостенный профиль, соединенный с оголовком самонарезающими винтами. Разрушение происходило в средней части и на опорах образца в результате потери местной устойчивости стенки и полок профиля (рис.10). При постепенном нагружении каждого испытываемого стержня наблюдаются характерные деформации полок и стенок профиля, которые неплохо согласуются с полученными в результате численных расчетов деформациями и распределением напряжений по длине элемента.
У тонкостенных стержней небольшой гибкости (λх ≤ 20) стенка или полка могут потерять устойчивость раньше, чем происходит потеря устойчивости стержня в целом. Потеря устойчивости каким-либо элементом сечения стержня (местная потеря устойчивости) и выход его из работы (даже частичный) резко ослабляют стержень, часто делая недеформированную часть сечения несимметричной. Центр изгиба при этом перемещается, стержень начинает закручиваться и быстро теряет устойчивость.
В результате испытаний получены предельные сочетания усилий N и M:
— на образец длиной 500 мм N = -26,000 кН; M = 7,3575 кН*см;
— на образец длиной 800 мм N = -25,000 кН; M = 13,0800 кН*см;
— на образец длиной 1000 мм N = -24,000 кН; M = 17,000 кН*см.
Предельные сочетания усилий N и M по результатам численного расчета:
— на образец длиной 500 мм N = -25,508 кН; M = 8,7351 кН*см;
— на образец длиной 800 мм N = -20,741 кН; M = 13,4137 кН*см;
— на образец длиной 1000 мм N = -24,046 кН; M = 15,550 кН*см.
Теоретические предельные сочетания усилий N и M по [19] без учета коэффициента γc составляют:
— на образец длиной 500 мм N = -37,558 кН; M = 12,8615 кН*см;
— на образец длиной 800 мм N = -32,809 кН; M = 21,2180 кН*см;
— на образец длиной 1000 мм N = -32,017 кН; M = 20,7050 кН*см.
Относительная разница натурных (численных) и теоретических результатов составила:
Погрешность может объясняться наличием случайного эксцентриситета при испытании или особенностями решающей программы.
Основные выводы:
- Действительная (опытная) несущая способность сжато-изогнутых стержней существенно отличается (см. п.2) от полученной по приближенным схемам, представленным в [18, 20] и получаемым по методике [19], в пределах (24÷32)%;
- Относительная разница результатов, полученных численным методом, и результатов расчета по методике [20] для моделей из прокатного двутавра показали следующее:
— для двутавра №10 гибкостью 18,52 ∆r = 1,522 от несущей способности по нормам;
— для двутавра №20 гибкостью 24,39 ∆r = 1,3551 от несущей способности по нормам;
— для двутавра №30 гибкостью 36,23 ∆r = 1,4360 от несущей способности по нормам;
— для двутавра №40 гибкостью 73,89 ∆r = 1,4670 от несущей способности по нормам;
- Относительная разница результатов, полученных численным методом, с результатами расчета по методике Айрумяна Э.Л. [19] без учета коэффициента условий работы γс для моделей ППЖ ПН-100-0,8 показали следующее:
— для стержня с гибкостью 20 составляет 0,3746 от несущей способности по [19];
— для стержня с гибкостью 40 составляет 0,4984 от несущей способности по [19];
— для стержня с гибкостью 60 составляет 0,6686 от несущей способности по [19];
— для стержня с гибкостью 80 составляет 0,8076 от несущей способности по [19];
— для стержня с гибкостью 100 составляет 0,9002 от несущей способности по [19];
— для стержня с гибкостью 120 составляет 0,9828 от несущей способности по [19].
- Получена близкая сходимость между результатами численных расчетов и результатами натурных исследований (в пределах 14%).
Библиографический список
- Karman T. Untersuchungen uber Knickfcstigkeit Mitteilungen uber For-schungsarbeiten auf dem geblete des Ingenieunvesens, №81, Berlin, 1910.
- Ros, Die Bemessung zentrisch u. exzentrisch gedruckten Stabe auf Kni-ckung Int. Kongress f. Bruck. u. Hochbau. Wien, 1928.
- Brunner J., Knickstabilitat, Schweizer Bauzeitung, т. 126, стр. 379, 1947.
- Геммерлинг А.В. и Климов П.И., Несущая способность центрально и внецеитренно сжатых стержней из стали марки НЛ2. Сборник ЦНИПС «Исследования по стальным конструкциям», Госстройиздат, 1956.
- Engesser F., Die Sicherung offener Brucken gegen Ausknicken, Zent-ralblatt der Bauverwaltung, 1884.
- Engesser F., Die Zusatzkrafte und Nebenspannungen elserner Fachwerkbrflcken, Berlin, 1893.
- Ясинский Ф.С, О сопротивлении продольному изгибу, Известия собрания путей сообщения, 1898.
- Ясинский Ф.С. Избранные работы по устойчивости сжатых стержней // Под ред. А.Н. Митинского. – М.: Гостехтеориздат, 1952.
- Ясинский Ф.С. Опыт развития теории продольного изгиба.
- Jasinski F.S., La flexion des pieces comprimees, Annaies des ponts et chaussees, 1894.
- Тимошенко С.П. Устойчивость упругих систем. – М.: Гостехиздат, 1955.
- Тимошенко С.П. Устойчивость стержней пластин и оболочек: Избранные работы // Под ред. Э.И.Григолюка. – М.: Наука, 1971.
- Timoshenko S., Stability and Strength of Thin-walled Constructions, Proc. 3d Intern. Cong. Applied Mechanics, т.3, стр. 1, Stockholm, 1930.
- Timoshenko S., Working Stresses for Columns and Thin-walled Structures. Trans. ASME, т. 55, Paper APM-55-20, 1932.
- Timоshenkо, Theory of Bending, Torsion and Buckling of Thin-walled Members of Open Cross Section, Jour. Franklin Inst., 1945.
- СНиП III-18-75. Металлические конструкции.
- Астахов И.В. Автореферат диссертации на соискание ученой степени кандидата технических наук. – СПб.: С.-Петерб. гос. архитектур.-строит. ун-т., 2006.
- Пособие по проектированию стальных конструкций (к СНиП II-23-81* “Стальные конструкции”) ЦНИИСК им. Кучеренко Госстроя СССР. — М.: ЦИТП Госстроя СССР, 1989. – 148 с.
- Айрумян Э.Л. Рекомендации по проектированию, изготовлению и монтажу конструкций каркаса малоэтажных зданий и мансард из холодногнутых стальных оцинкованных профилей производства ООО конструкций «БалтПрофиль». – М.: ЦНИИПСК им.Мельникова, 2004.
- СНиП II-23-81*. Стальные конструкции. Нормы проектирования / Госстрой России. – М.: ГУП ЦПП, 2001.