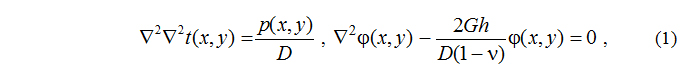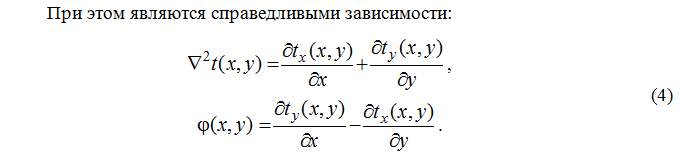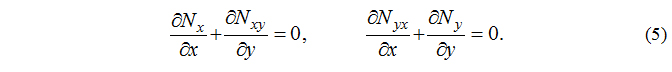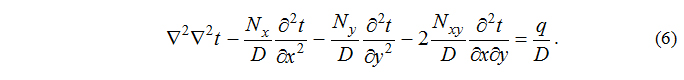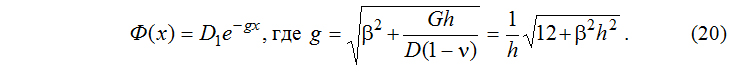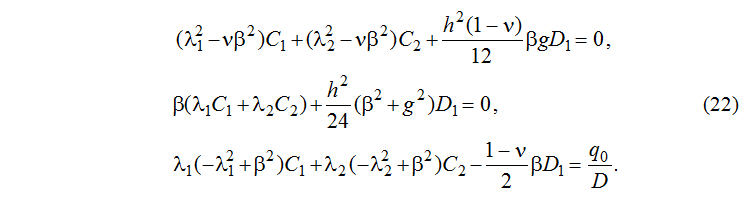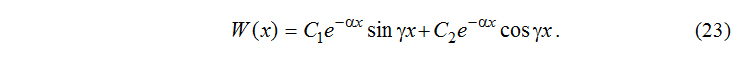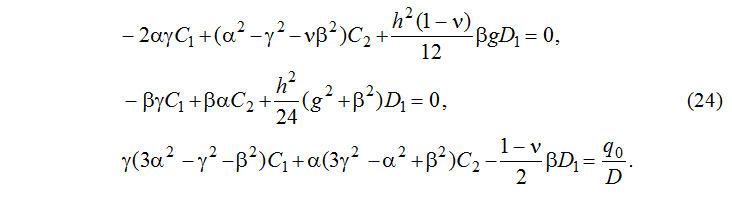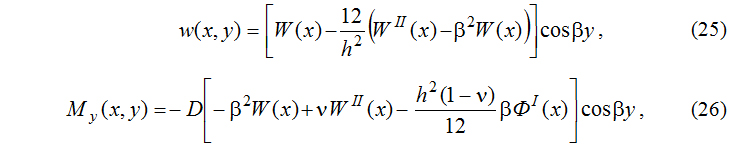Леонтьев А.Н. – Профессор кафедры «Испытания сооружений» Московского государственного строительного университета,
кандидат технических наук
Бен Хелал Монсеф – Аспирант кафедры «Испытания сооружений»
Московского государственного строительного университета
Вагиалла Хасан Ахмед Мохаммед – Аспирант кафедры «Испытания
сооружений» Московского государственного
строительного университета
Напряженное и деформированное состояние плиты средней толщины при ее изгибе от действия поперечной нагрузки описывается, как известно [1], уравнениями:
где G – модуль упругости второго рода материала плиты;
D, h, v – соответственно ее цилиндрическая жесткость, толщина и коэффициент Пуассона.
Искомые функции t(x,y), связаны с прогибом w(x,y) и углами поворота tx(x,y), ty(x,y) выражениями:
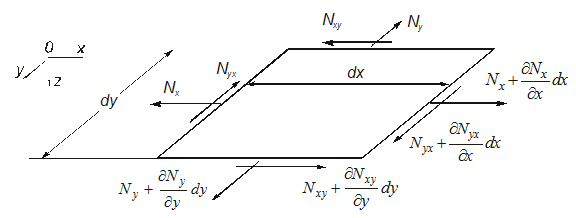
В случае учета, кроме поперечной нагрузки q(x,y), сил Nx, Ny, Nxy=Nyx, действующих в срединной плоскости плиты (рис.1), второе из уравнений (1) остается неизменным, а к первому должны быть добавлены проекции этих сил на ось Оz, возникающие за счет изгиба плиты. Заметим, что эти силы связаны между собой уравнениями равновесия:
Спроецируем силы Nx, Ny, Nxy=Nyx и их приращения на вертикальную ось. Тогда первое из уравнений (1) с учетом выражений (3) – (5) можно записать в виде:
Будем считать, что продольные края рассматриваемой плиты шарнирно оперты (рис.2). При этом искомые функций могут быть представлены в виде:
Подставляя разложение (7) в уравнение (6), в силу ортогональности тригонометрических функций для каждого номера n получим обыкновенное дифференциальное уравнение четвертого порядка, которое при действии только продольных сил Nx запишется в виде:
В зависимости от соотношения величин коэффициентов rn и sn определяется вид корней соответствующего характеристического уравнения и, следовательно, вид частных интегралов, составляющих его решение.
Рассмотрим вначале случай загружения плиты силами Ny, равномерно распределенными по ее продольным краям (см. рис.2). Из сопоставления уравнений (10) и (11) можно видеть, что коэффициентами уравнения (11) в этом случае будут величины:
Рассмотрим теперь задачу об изгибе полубесконечной плиты, загруженной в начальном сечении поперечной нагрузкой q(y) и продольными сжимающими силами Ny, равномерно распределенными по продольным краям (см. рис.2).
В этом случае, если заданная поперечная нагрузка представлена выражением qy=cosβy, где β=π/b, то уже один первый член разложения (7) будет представлять точное решение, в результате чего индекс n всюду может быть опущен. Учитывая бесконечную протяженность плиты, решение уравнения (11) можно представить в виде:

Для полного решения задачи об изгибе плиты средней толщины к выражению (19) необходимо добавить еще интеграл второго из уравнений (1), который с учетом разложения (8) и бесконечности плиты может быть записан в виде:
Для определения трех постоянных интегрирования C1, C2, D1 в начальном сечении (x = 0) могут быть сформулированы следующие граничные условия:
Раскрывая эти условия при помощи выражений (19) и (20), получим систему трех алгебраических уравнений:
Рассматривая ту же задачу при наличии растягивающих сил Ny, решение (15) можно записать в виде:
Для определения постоянных интегрирования граничные условия (21) и выражения (20) и (23) позволяют записать следующие уравнения:
После решения систем уравнений (22) и (24) и нахождения постоянных C1, C2, D1 все расчетные величины определяются по формулам теории изгиба пластинок средней толщины [1]. Так например, прогиб плиты w(x,y) и изгибающий момент My(x,y) определяются в виде:
(23) при растяжении.т величины безразмерных продольных усилий N̄y= Nyb2/D. Сплошные линии 1 и 2 относятся здесь, соответственно, к случаям сжатия и растяжения плиты средней толщины при h/b = 0,2 и = 0,2, а пунктирные линии 3 и 4 – к случаям сжатия и растяжения тонкой плиты.
где входящая в (25) и (26) функция W(x) имеет вид (19) при сжатии плиты и вид (23) при растяжении.
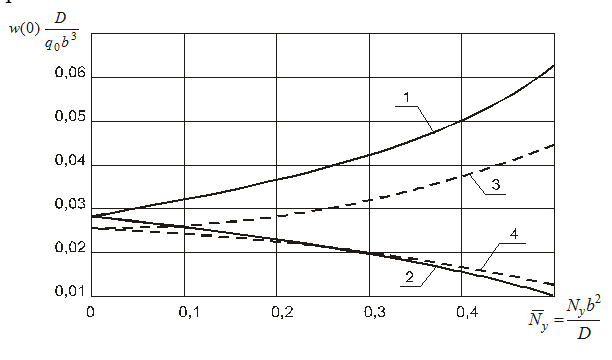
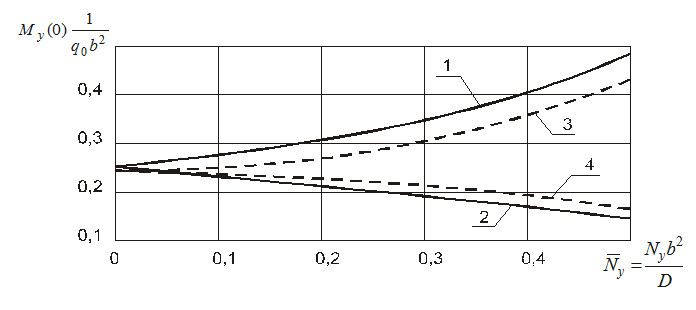
На рис.3 и рис.4 приведены кривые, показывающие зависимость величины прогиба w(0) и изгибающего момента My(0) в середине загруженного края плиты от величины безразмерных продольных усилий Ny= Nyb2/D. Сплошные линии 1 и 2 относятся здесь, соответственно, к случаям сжатия и растяжения плиты средней толщины при h/b = 0,2 и = 0,2, а пунктирные линии 3 и 4 – к случаям сжатия и растяжения тонкой плиты.
Можно видеть, что увеличение продольных усилий Ny приводит к существенному изменению значений прогиба и изгибающих моментов: увеличению при сжатии и уменьшению при растяжении. При этом в процентном отношении прогибы изменяются более интенсивно, чем изгибающие моменты. Следует отметить также, что влияние продольных усилий на прогибы плиты средней толщины оказывается несколько большим, чем на прогибы тонкой плиты и большим при сжатии, чем при растяжении. При этом линии 1 и 3, близкие к прямым при малых значениях Ny, становятся криволинейными с тенденцией к резкому возрастанию при увеличении Ny и приближением их значений к критическим.
Библиографический список
- Власов Б.Ф. Уравнения изгиба плит средней толщины // Теоретические и экспериментальные исследования прочности и жесткости элементов строительных конструкций. – М.: МИСИ, 1989.
- Габбасов Р.Ф., Филатов В.В. Расчет сжато-изогнутых пластин при неполном контакте с упругим основанием // Сб. трудов МГСУ. – М., 1999.
- Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. – М.: Наука, 1966.
- Турганбаев А.Т. Изгиб прямоугольной плиты, лежащей на упругом основании Винклера с учетом влияния продольных усилий // Основания, фундаменты и механика грунтов. 1993, №3.
от величины безразмерных продольных усилий N̄y= Nyb2/D. Сплошные линии 1 и 2 относятся здесь, соответственно, к случаям сжатия и растяжения плиты средней толщины при h/b = 0,2 и = 0,2, а пунктирные линии 3 и 4 – к случаям сжатия и растяжения тонкой плиты.