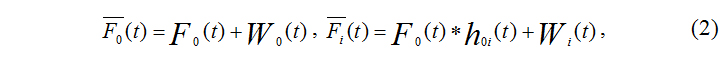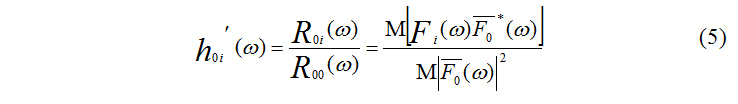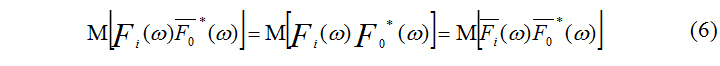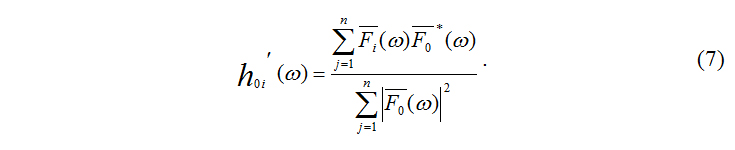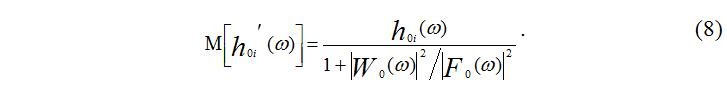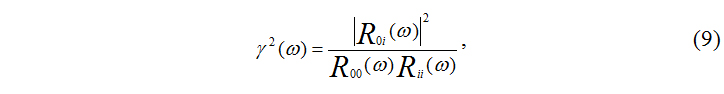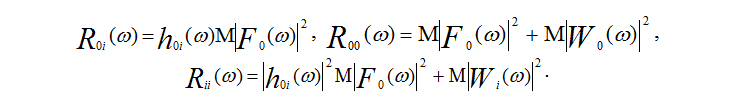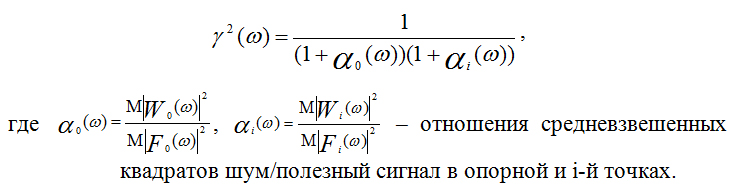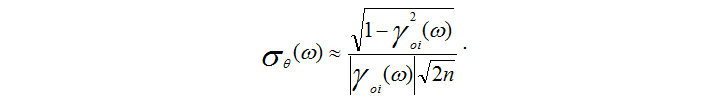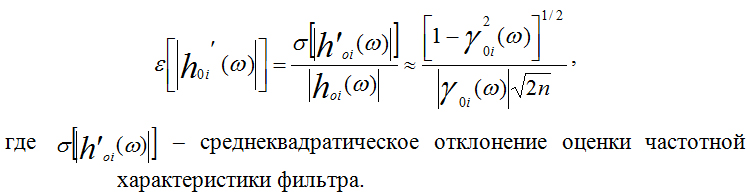Еманов Александр Федорович – Директор Алтае-Саянского филиала
Геофизической службы СО РАН, доктор технических наук
Селезнёв Виктор Сергеевич – Директор геофизической службы СО РАН,
доктор геолого-минералогических наук
Бах Александр Александрович – Старший научный сотрудник
геофизической службы СО РАН
Инженерные сооружения по конструкции являются замкнутым объёмом, и распространение сейсмических колебаний в них приводит к формированию стоячих волн. Ещё в девятнадцатом веке была доказана общеизвестная теорема [6, 8, 9] о независимости решения по стоячим волнам от начальных условий. Для инженерных сооружений это означает, что стоячие волны, формирующиеся в них, не зависят от источника колебаний. Для поля стоячих волн в здании не важно, где размещён источник колебаний и какого типа источник используется.
Опираясь на данную теорему, можно сказать, что детальность и точность исследования стоячих волн в инженерных сооружениях должны быть одинаковы независимо от того, изучаем мы микросейсмические колебания или применяем высокостабильные по излучению искусственные источники колебаний. До последнего времени в экспериментах по изучению зданий и сооружений измерения на микросейсмических колебаниях обосновано считались менее точными, чем исследования с искусственными источниками. Дело в том, что принципиальные возможности метода и практическая реализация не всегда совпадают.
В данной работе обосновывается методика наблюдений за микросейсмами в инженерном сооружении, создаётся математическая модель волнового поля, строятся алгоритмы, позволяющие выделить стоячие волны в чистом виде и преобразовывать их из разновремённых наблюдений в одновременные записи стоячих волн на плотной системе наблюдений в инженерном сооружении. Рассматриваются возможности качественной интерпретации детальной информации о стоячих волнах для диагностики физического состояния и определения сейсмостойкости сооружений, а также затрагиваются проблемы разработки методов количественной интерпретации детальных наблюдений.
Колебания для каждой из нормальных мод описываются выражением [х]
y(x, y, z, t) = A(x, y, z) cos(wmt + φx,y,z), (1)
где A(x, y, z) – геометрическая форма стоячей волны;
φx,y,z – фаза колебаний в заданной точке для конкретной нормальной моды;
wm – частота собственных колебаний.
Геометрическая форма стоячей волны, фаза и частота собственных колебаний зависят от строения инженерного объекта, от физических параметров материала, из которого изготовлено сооружение. При детальном измерении в объёме инженерного сооружения колебаний на каждой из нормальных мод мы можем изучить строение объекта и выявить возникающие в нём дефекты и ослабленные места. Такие исследования можно отнести к сейсмической дефектоскопии инженерных сооружений.
Стандартная оценка сейсмостойкости зданий основана на определении усиления колебаний в здании на частотах наиболее интенсивных нормальных мод [7]. Детальное изучение стоячих волн в инженерном сооружении – это не только определение дефектов в здании, но и новый уровень точности и детальности в оценке сейсмостойкости.
Из уже упомянутой теоремы вытекает важное свойство когерентности во времени колебаний в стоячих волнах. По стоячим волнам линейная связь между записями колебаний двух точек не зависит от времени. И эта связь выполняется как для амплитуд, так и для фаз стоячих волн. Отмеченное свойство когерентности во времени мы будем использовать для создания методики детального изучения характеристик стоячих волн в инженерных сооружениях.
Для детального изучения стоячих волн в инженерном сооружении необходимо решить два актуальных вопроса. Если мы установим сейсмоприёмник в здании, то будем регистрировать сумму стоячих и бегущих волн. Первый вопрос: как выделить из регистрируемых колебаний стоячие волны? Детальное изучение стоячих волн в инженерном сооружении требует плотных систем наблюдений. При обследовании крупных сооружений потребуются сотни и даже тысячи точек с одновременными записями стоячих волн. Второй вопрос: как обойтись для изучения стоячих волн в инженерном сооружении на плотной системе наблюдений, измерениями с малоканальной аппаратурой?
Основу решения поставленных задач составит метод восстановления когерентных составляющих сейсмических волновых полей [3], позволяющий выделять когерентные волны из экспериментально наблюдаемых волновых полей. В упомянутой работе введено понятие когерентность по параметру. Дело в том, что, когда мы говорим о линейной связи между сейсмическими записями, то независимой она может быть от любого параметра, например, по измерению в пространстве, по элементам системы наблюдений, по площади, по энергии и т.п. Когерентность по времени – это частный случай когерентных сигналов.
Для детального обследования здания с использованием микросейсм идеально реализовать плотную систему одновременной регистрации колебаний, но это не представляется возможным. Рассмотрим иную систему наблюдений и её возможности. Одновременная регистрация колебаний здания под воздействием микросейсм ведётся в опорной и i-й точках (группе точек), затем i-я точка (группа точек) меняет свое положение и вновь проводится регистрация сейсмических колебаний одновременно с опорной точкой. Такими наблюдениями можно детально покрыть исследуемый объект с малоканальной аппаратурой.
Задача состоит в том, как преобразовать разновремённые наблюдения в разных точках здания в одновременную запись стоячих волн на всей системе наблюдений. Для решения этой задачи необходима математическая модель колебаний. Представим колебания каждой точки как сумму двух составляющих. Первая составляющая – стоячие волны, вторая – бегущие волны.
Заложим в основу модели сейсмических колебаний инженерных сооружений, следующие предположения:
1. При воздействии микросейсмических колебаний на здание (инженерное сооружение) отличия формирующихся в нём стоячих волн, зарегистрированных в двух произвольных точках, описываются линейной системой, характеристика которой не зависит от времени.
2. При воздействии микросейсмических колебаний на здание отличия бегущих волн, зарегистрированных в двух произвольных точках, не могут быть описаны линейной системой, характеристика которой не зависит от времени.
3. Линейные связи в изменениях стоячих волн, регистрируемых в двух точках, существуют для каждой пары одноимённых компонент регистрируемых колебаний.
Третье предположение существенно упрощает поставленную задачу. Вместо того, чтобы работать с векторными сигналами с девятью характеристиками связи, мы будем работать с данными регистрации по каждой из компонент колебаний независимо друг от друга и обойдёмся тремя характеристиками связи.
Модель связи колебаний, регистрируемых в двух разных точках инженерного сооружения (здания), примет вид
где h0i(t)– импульсная характеристика линейной системы, описывающей связь между одновременными записями стоячих волн в точках 0 и i на обследуемом объекте;
W(t)– бегущие волны;
F0(t)– запись стоячей волны в опорной точке.
Подход к обработке инженерно-сейсмологических данных рассматриваемый в данной работе является развитием работ [2-5].
Для модели процесса колебаний в здании есть возможность получить одновременные записи стоячих волн из разновремённых, последовательных наблюдений с опорной точкой. Процедура обработки в таком случае сводится к следующим операциям.
1. Нахождение частотных характеристик линейных систем h0i(w).
2. Запись или формирование независимой реализации процесса колебаний опорной точки при сейсмическом воздействии на исследуемый объект.
3. Пересчёт стоячих волн из опорной точки с использованием h0i(w) во все точки обследуемого объекта.
Ключевым вопросом рассматриваемой схемы является задача определения h0i(w) с необходимой точностью по записям микросейсмических колебаний. Рассматривая модель сигналов, регистрируемых в двух точках здания на одинаковых компонентах, можно видеть, что задача определения h0i(w) сводится к определению характеристики линей
ной системы по сигналам на её входе и выходе, зарегистрированных на фоне шумов. Фактически необходимо определить характеристику фильтра, обеспечивающего наилучший пересчёт стоячих волн из опорной точки в i-ю.
Взяв производную по h0i/(t)от данного выражения и приравняв её к нулю, получим
Осуществив преобразование Фурье и перейдя в частотную область, получим
В знаменателе выражения (5) стоит усреднённый квадрат модуля спектра колебаний в опорной точке. Решив, каким образом осуществляется усреднение, можно осуществить его вычисление. В числителе выражения (5) стоит усреднённый взаимный спектр колебаний в опорной точке и стоячей волны в i-й точке. Fi(t) экспериментально не измеряется. Приняв, что W0(t) и Wi(t) являются стационарными, случайными процессами, некоррелированными друг с другом и с записями стоячих волн в опорной и i-й точках, легко доказывается, что [1]
Выражение (6) позволяет подставить в числитель формулы (5) усреднённый взаимный спектр колебаний, зарегистрированных одновременно в опорной и i-й точках.
Усреднение спектров в данной ситуации можно осуществить, разбивая реализацию колебаний, записанных одновременно, на n блоков. Разбив на неперекрывающиеся блоки запись, получаем множество реализаций, по которым можно осуществить усреднение. Формула для расчёта фильтра Винера, обеспечивающего пересчёт колебаний из опорной точки в i-ю, примет вид
Отличия частотной характеристики фильтра Винера от характеристики линейной системы, описывающей различия стоячих волн в двух точках обследуемого объекта, описываются смещённостью оценки, которая определяется отклонением математического ожидания определяемой частотной характеристики от истинного её значения. Можно показать, что
В соответствии с (8) частотная характеристика фильтра является смещённой оценкой характеристики линейного фильтра, описывающего связь колебаний двух точек обследуемого объекта. Смещённость оценки выражается в регуляризации фильтра по соотношению шум/сигнал. Другими словами, фильтр запирается на частотах с низким соотношением сигнал/шум. Отметим, что оценка фазовой характеристики фильтра не смещена.
Формула (7) позволяет вести расчёт характеристики фильтра с погрешностью, которая зависит от следующих параметров наблюдений: шаг дискретизации по времени – Δt, длина единичного блока – Т, количество блоков в записи – n. Выбор первых двух параметров не вызывает затруднений. Шаг дискретизации увязывается с частотным диапазоном, в котором изучается реакция объекта на сейсмическое воздействие. Длина единичного блока связана с необходимым разрешением спектрального анализа Δf=1/T. Сложнее вопрос о количестве блоков. Расчёт по формуле (7) – лишь некоторая оценка характеристики фильтра, погрешность которой зависит от количества блоков n и соотношения энергии шумов и полезных сигналов в модели (2).
Для оценки количества блоков, необходимых для обеспечения заданной погрешности фильтра, полезен спектр когерентности g(w), который можно рассчитать по записям микросейсмических колебаний в двух точках обследуемого объекта по формуле
где R00(w) – спектр автокорреляционной функции колебаний, записанных в опорной точке;
Rii(w) – тоже в i-й точке.
Применяя модель (2), получим:
Эти выражения получены в предположении о независимости реализаций шумов на входе и выходе линейной системы и их некоррелированности с полезными сигналами. Подставляя полученные соотношения в (9), получим
Из формулы (10) следует, что спектр когерентности зависит только от отношения энергии бегущих волн к энергии стоячих волн. Спектр когерентности может быть рассчитан по одновременным записям в любой паре точек обследуемого объекта. Значения g(w) лежат в диапазоне 0-1. Единица соответствует случаю, когда в двух точках регистрируются только стоячие волны. При g(w)=0 в двух точках здания регистрируются только бегущие волны.
Экспериментами доказано [2-5], что значения спектра когерентности на собственных частотах инженерных сооружений высоки 0.8-0.99, а в промежутке между ними соответствуют значениям 0.1-0.3.
Полученный алгоритм расчёта характеристики фильтров является симбиозом фильтра Винера, свойства когерентности стоячих волн и методов математической статистики. Математическая статистика позволяет не только строить фильтры для выделения когерентных во времени стоячих волн, но и определять точность полученного волнового поля через дисперсию оценки характеристик. Подробное описание алгоритмов оценки точности можно найти в работе [4]. Среднеквадратическая ошибка фазовой характеристики фильтра Винера для пересчёта стоячих волн из опорной точки в i-ю будет равна
Данная формула позволяет рассчитать ошибку фазовой характеристики в зависимости от частоты в радианах. Относительная ошибка амплитудной характеристики фильтра равна
Из этих формул заданная точность и число блоков могут быть увязаны после вычисления значения спектра когерентности на частоте собственных колебаний здания. Количество блоков определяет длину реализации, записанную в каждой точке обследуемого объекта, и существенно влияет на производительность работ. Оптимальная производительность достигается последовательной регистрацией колебаний в точках объекта при длине реализации 5-10 минут и существенно снижается при длинах реализаций, измеряемых часами. При высокой когерентности колебаний 0.8-0.99, наблюдаемой на инженерных сооружениях на частотах нормальных мод, удаётся достигнуть погрешности порядка 5% и менее для пересчёта стоячих волн и производительности обследования зданий – за несколько дней, а такого объекта, как плотина Саяно-Шушенской ГЭС, – за две недели (при детальности обследования через 5-10 м).
Пример восстановления поля стоячих волн дан на рис.1. На рисунке приведены разновременные наблюдения в одной из галерей Саяно-Шушенской ГЭС (рис.1,а), трассы пересчитанных в эти же точки системы наблюдений колебаний (рис.1,б), результат двухмерной фильтрации пересчитанных трасс (рис.1,в). Вместо нерегулярных колебаний мы получили регулярное волновое поле, в котором явно видны отражения от бортов плотины.
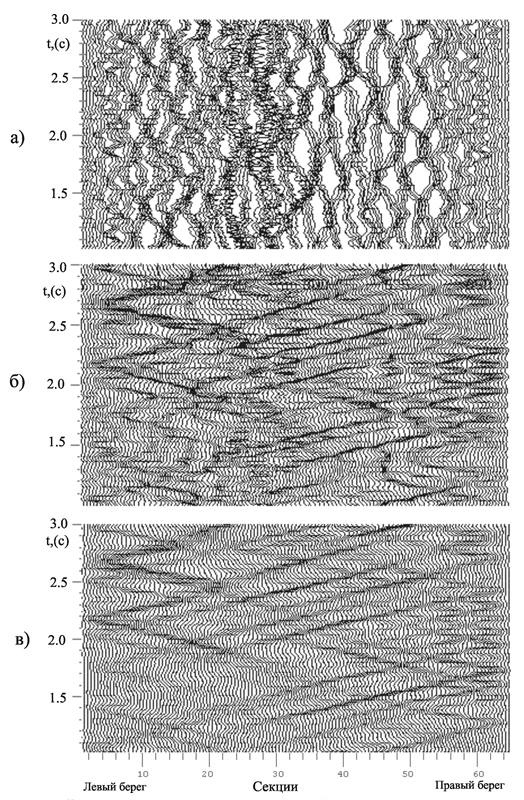
Рис.1. Пример пересчёта стоячих волн из опорной точки в другие точки системы наблюдений: а – разновремённые записи микросейсмических колебаний в галерее плотины Саяно-Шушенской ГЭС (отметка 521 м); б – результат пересчёта стоячих волн из опорной точки в фрагмент системы наблюдений, соответствующий а; в – двумерная фильтрация б
По этим записям начинается детальное обследование. Первый вопрос обследования – это обнаружение и изучение нормальных мод колебаний инженерного сооружения. На рис.2 дан монтаж спектров трасс вдоль одной из галерей плотины Саяно-Шушенской ГЭС (радиальные колебания). По спектрам модуляция амплитуды от трассы к трассе позволяет сразу же определять кратность обнаруженной моды. Для таких объектов, как плотины ГЭС, предложенная методика позволяет выявлять и изучать особенности распределения амплитуд и фаз стоячих волн по пространству на нескольких десятках нормальных мод.
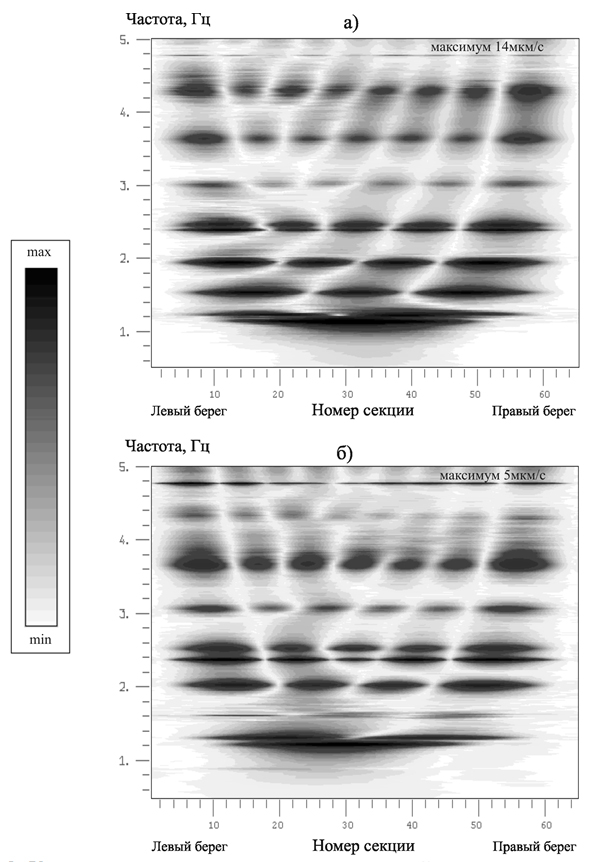
Рис.2. Карты амплитудных спектров радиальной скорости смещения пересчитанных колебаний в одну из галерей Саяно-Шушенской ГЭС (отметка 521 м). Длина секции 15 м: а – для уровня воды в водохранилище 539 м; б – для уровня воды в водохранилище 500 м
Выделенные стоячие волны легко отфильтровываются и строятся карты амплитуд и фаз колебаний по каждой из нормальных мод в обследуемом объекте. По ним изучаются особенности каждой из стоячих волн. При обследовании зданий основная информация содержится в искажениях геометрической формы стоячей волны, вызванных физическим состоянием конструкций. Анализ искажений позволяет проводить диагностику физического состояния зданий и выявлять элементы наиболее вероятных разрушений при сейсмических воздействиях.
Заключение
1. Разработаны алгоритмы восстановления одновременных записей стоячих волн в инженерных сооружениях по разновремённым измерениям микросейсмических колебаний с записями опорных колебаний в одной или нескольких точках, а также алгоритм оценки точности, в основе которых заложены методы Винеровской фильтрации, свойство когерентности стоячих волн во времени и методы статистического оценивания характеристик.
2. Экспериментально доказаны высокая точность и детальность восстановления стоячих волн в инженерных сооружениях как по пространственным измерениям, так и по шкале частот колебаний.
3. Созданная методика детального изучения стоячих волн в инженерных сооружениях является основой диагностики физического состояния зданий и сооружений и изучения их сейсмостойкости на уровне элементов конструкций.
Библиографический список
- Бендат Дж., Пирсол А. Измерение и анализ случайных процессов. М.: Мир, 1971, 408 с.
- Еманов А.Ф. О применении вибраторов для определения сейсмостойкости зданий и в микросейсморайонировании. Геология и геофизика, 1995, №7. С.87-92.
- Еманов А.Ф., Селезнёв В.С. Пересчёт колебаний фильтрами Винера как основа универсального метода обработки сейсмических волн.// Проблемы сейсмологии ІІІ тысячелетия: Материалы международной геофиз. конф., г.Новосибирск, 15-19 сент. 2003г.-Новосибирск: Издательство СО РАН, 2003. – С.207-231.
- Еманов А.Ф., Селезнёв В.С., Бах А.А. и др. Пересчёт стоячих волн при детальных инженерно-сейсмологических исследованиях / Геология и геофизика, 2002. №2. С.192-207.
- Еманов А.Ф., Бах А.А., Данилов И.А. и др. Детальные инженерно-сейсмологические исследования плотины Саяно-Шушенской ГЭС. – Вестник Красноярской государственной архитектурно-строительной академии: Сб. науч. тр. Вып.6/ Под ред. В.Д. Наделяева. – Красноярск: КрасГАСА, 2003. C.86-108.
- Крауфорд Ф. Волны. // Берклиевский курс физики. – Т.3. М.: Наука. 1976, 526 с.
- Медведев С.В. Инженерная сейсмология. – М.: Изд-во литературы по строительству, архитектуре и строительным материалам. 1962. – 283 с.
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Т.3. Излучение. Волны. Кванты// – М.: Мир, 1976. 496 с.
- Пейн Г. Физика колебаний и волн. – М.: Мир, 1979. 387 с.