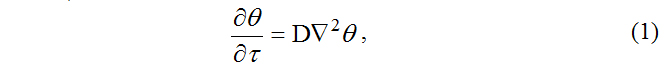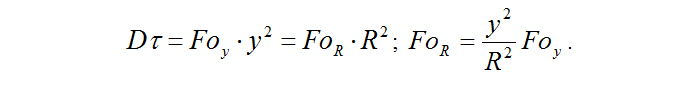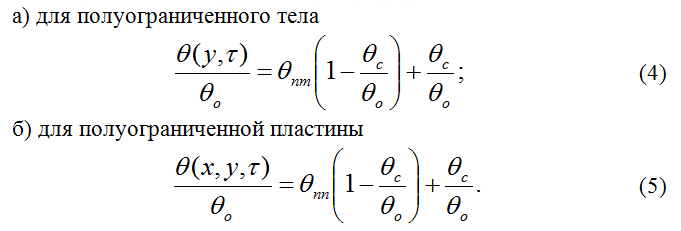Новичков Петр Игнатьевич – Профессор кафедры «Строительные конструкции»
ГОУ ВПО «Мордовский государственный университет им. Н.П. Огарева»,
кандидат технических наук, доцент
Железобетонные конструкции в процессе эксплуатации могут подвергаться экстремальным воздействиям или повышенных температур при высокоинтенсивном нагреве (пожаре), или повышенной влажности при переменном увлажнении и высыхании, или концентрации агрессивной среды химического или биологического происхождения. Все эти воздействия сопровождаются или переносом теплоты вследствие градиента температуры, или переносом вещества (компонента смеси) при наличии градиента его концентрации. Явления переноса, необратимые процессы, в результате которых в физической системе происходит пространственный перенос энергии, массы, импульса, энтропии или какой-либо другой физической величины. Причинами явлений переноса являются или действие внешних полей, или наличие пространственных неоднородностей температуры, состава или средней скорости движения частиц системы. Перенос физической величины происходит в направлении, обратном её градиенту, то есть таким образом система приближается к состоянию равновесия.
Явления переноса описываются законом Фурье при переносе теплоты теплопроводностью или законом Фика при переносе вещества (компонента вещества определённой концентрации) диффузионным потоком. В первом случае процесс сопровождается выравниванием температуры, во втором случае выравниванием распределения концентрации переносимого вещества (компонента вещества определённой концентрации). Так как математическое оформлениеэтих законов тождественно целесообразно оперировать величиной Θ, которую называют переносом потенциала, а процесс, сопровождающий перенос данной величины – потенциалопроводностью. Под потенциалом Θ понимается или температура t при переносе теплоты теплопроводностью или потенциал переноса массы М (компонента смеси определённой концентрации С) при переносе вещества (компонента смеси) диффузией.
Из большого количества номенклатуры железобетонных конструкций остановимся на ребристых и многопустотных плитах перекрытия и на их примере покажем влияние формы поперечного сечения на эксплуатационный срок службы элементов.
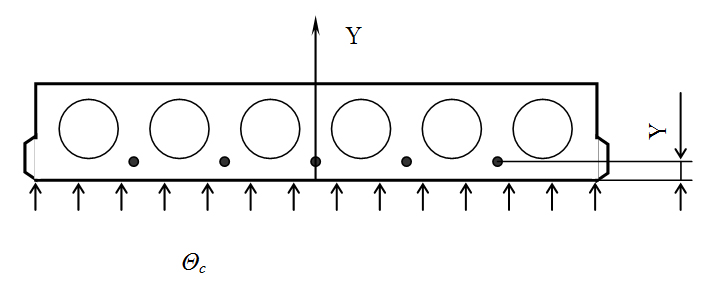
Несущая продольная арматура в ребристых плитах перекрытия располагается в продольных ребрах (рис. 1). В процессе эксплуатации бетон ребра плиты с расположенной в нем арматурой подвергается воздействию среды с трех сторон: с нижней и боковых поверхностей. Арматура относительно боковых поверхностей располагается симметрично (в середине), следовательно, продольное ребро при симметричном воздействии среды с боковых поверхностей можно идеализировать как неограниченную пластину. Толщина защитного слоя бетона снизу составляет около 10% высоты плиты и соответственно ребра. Такое соотношение между размером тела и координатой интересующей нас точки дает право идеализировать продольное ребро при воздействии среды с нижней поверхности как полуограниченное тело. Комбинация неограниченной пластины с полуограниченным телом в теории массопереноса соответствует полуограниченной пластине. Характеристическими размерами для полуограниченной пластины являются величины у и R, причем у относится к полуограниченному телу, а R – к неограниченной пластине.

Рис. 1. Математическая модель продольного ребра ребристой плиты перекрытия при воздействии внешней среды
В многопустотной плите перекрытия с унифицированной высотой 220 мм продольная арматура располагается на расстоянии 20-25 мм от нижней поверхности (рис. 2). При таком положении арматуры плита при воздействии агрессивной среды с нижней поверхности приводится к математической модели полуограниченного тела, характеристическим размером для которого является координата у.
Дифференциальное уравнение переноса потенциала q, или потенциалопроводности, аккумулирующего в себе и закон теплопроводности Фурье, и закон диффузии Фика [1, 2] (без учета тепло- и бародиффузии и при отсутствии внутренних источников или стоков тепла или массы), запишется в виде
где I – значение потенциала переноса как функции времени и координат;
τ – время;
D – эквивалентный коэффициент потенциалопроводности.
Решение уравнения (1) при граничных условиях первого рода запишется следующим образом:
На рис. 3 приведены зависимости изменения относительных значений потенциалов переноса для полуограниченного тела и полуограниченной пластины. Эти зависимости представлены как функции относительного значения потенциала переноса на поверхности для различных значений чисел Фурье Foi. Значения чисел Фурье, безразмерного времени, представленные на графике, отражают возможные пределы изменения эквивалентного коэффициента потенциалопроводности бетона при величине защитного слоя его в пределах от 5×10-3 до 5×10-2 м. За базовые значения чисел Фурье приняты значения в направлении оси Y, как для полуограниченного тела – Fo = Dτ / у2(см. рис. 1 и 2). Тогда значение числа Фурье (при равнозначном эквивалентном коэффициенте потенциалопроводности D), как фиксированного времени FoR, в направлении оси Х для полуограниченной пластины найдем из равенства (см. рис. 1):
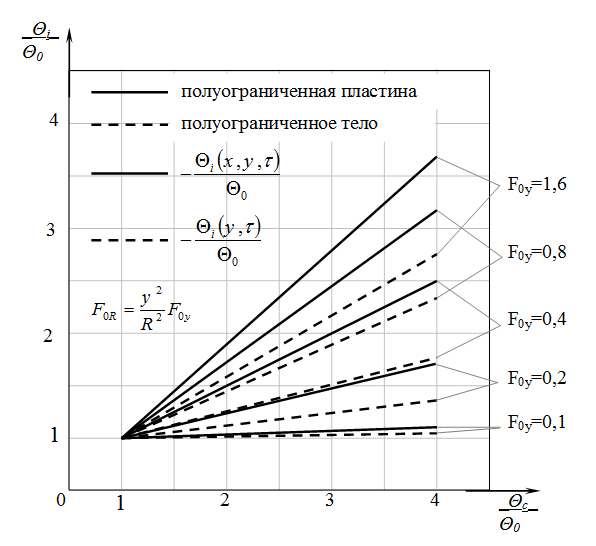
Рис. 3. Зависимость изменения относительных значений потенциалов переноса в полуограниченной пластине и в полуограниченном теле для различных значений чисел Фурье
Относительные величины потенциалов переноса внутри рассматриваемых тел в зависимости от параметров потенциалопроводности Qi и относительного потенциала на поверхности тел Qс/Qo, полученные из выражений (2, 3) будут иметь вид:
Анализ зависимостей изменения относительного значения потенциала переноса qi/qo от относительного значения потенциала переноса среды на поверхности тела qс/qo показывает следующее. Все прямые сходятся в одной точке с координатами qi/qo = qс/qo = 1, соответствующей равновесному состоянию полуограниченного тела и полуограниченной пластины с окружающей средой. Равенство относительных значений потенциалов переноса внутри тел и на поверхности свидетельствует об отсутствии внутреннего переноса потенциала и какого-либо взаимодействия окружающей среды с материалом тел.
Увеличение относительного потенциала среды на поверхности тел стимулирует внутренний его перенос. Изменения относительных значений потенциалов переноса внутри тела qi/qo от увеличения значений потенциала переноса на поверхности тела подчиняются линейным зависимостям при всех значениях Foi.
Сравнительный анализ относительных значений потенциалов переноса для полуограниченного тела qi(y,t)/qo и полуограниченной пластины qi(х,у,t)/qo показывает следующее. Например, при относительном значении потенциала переноса на поверхности qс/qo = 4, относительное значение диффундирующего потенциала среды внутри полуограниченной пластины достигает значения переноса qi(х,у,t)/qo = 2,5 при Foуnn = 0,4. То же относительное значение потенциала переноса внутри полуограниченного тела qi(y,t)/qo = 2,5 достигается при числе Foуnm = 1,2. Это свидетельствует о разных скоростях кинетики происходящих процессов внутри полуограниченного тела и внутри полуограниченной пластины при равнозначных начальном и граничных условиях для них. Если координаты Y, равные расстоянию от нижний поверхностей до рассматриваемой точки, например, до расположения продольной арматуры, для полуограниченного тела и для полуограниченной пластины одинаковы, то время достижения относительных значений потенциалов переноса qi(y,t)/qo = qi(х,у,t)/qo = 2,5 (при равных обменных параметрах) для полуограниченной пластины будет в три раза меньше Foуnm / Foуnn = 1,2/0,4 = 3, чем для полуограниченного тела. Такое же соотношение, при котором время достижения равных относительных значений потенциалов переноса в полуограниченной пластине меньше, чем в полуограниченном теле (при равнозначных обменных параметрах) начальном и граничных условиях, наблюдаются для всех чисел Fо. С увеличением числа Fо это соотношение увеличивается с 1,7 при Fоу = 0,1 до 5 и более при Fоу = 0,8 и более.
Перенесем результаты анализа полуограниченных тела и пластины на реальные конструктивные элементы: многопустотную и ребристую плиты перекрытия. Сравним их сроки службы при конкретном относительном значении потенциала среды, например, при qс/qo = 4, при равнозначности всех потенциалообменных параметров бетона плит и одинаковой толщине защитного слоя бетона для продольных арматур в многопустотной плите и в продольном ребре ребристой плиты. При анализе будем основываться также на предположении, что кинетика изменения механических и деформативных характеристик бетона и арматуры под действием проникающего потенциала среды находится в прямой зависимости от ее относительного значения. Результаты сравнительного анализа изменения относительных значений потенциалов переноса в полубесконечные тело и пластину при учете вышеизложенных допущений показывают, что срок службы ребристой плиты перекрытия должен быть в 3-5 раз меньше срока службы многопустотной плиты перекрытия.
Для получения равнодолговечных ребристой и многопустотной плит перекрытия необходимо изменить конструктивные параметры, например, толщину защитного слоя бетона или физические параметры бетона ребристой плиты. Физический параметр в виде эквивалентного коэффициента потенциалопроводности D и толщины защитного слоя бетона объединяются со временем в одном критерии подобия – безразмерном времени – числе Фурье Fo. Например, для полуограниченного тела, идеализирующего многопустотную плиту перекрытия, относительное значение потенциала переноса в теле, равное qi(y,t)/qo = 2,5, достигается при Foуnm = 1,2 для относительного значения потенциала переноса среды qс/qo = 4. Для полуограниченной пластины, идеализирующей ребро ребристой плиты, то же относительное значение потенциала переноса при равнозначных условиях достигается при Foуnn = 0,4. При условии равнодолговечности, когда tпт = tпп, число Foуnn для полуограниченной пластины при равных значениях эквивалентного коэффициента потенциалопроводности найдем из условия, что
Рассмотренная в данной работе методика оценки формы поперечного сечения позволяет выбрать оптимальное конструктивное решение с учетом условий последующей эксплуатации. Данная методика применима для оценки различных форм поперечных сечений, идеализируемые, например, в виде прямоугольника, тавра, круга [3, 4].
Библиографический список
- Лыков, А.В. Теория теплопроводности [Текст]/ А.В.Лыков.-М.: Высшая школа, 1967. – 600с.
- Франк – Каменецкий, Д.А Диффузия и теплопередача в химической кинетике [Текст]/ Д.А. Франк – Каменецкий. М.: Наука, 1967.-491с.
- Новичков, П.И. Теоретические основы оценки конструкционных и эксплуатационных свойств поперечных сечений железобетонных конструкций, испытывающих воздействие потенциала переноса, на стадии проектирования [Текст]/ П.И.Новичков // Известия ТулГУ. Серия. Строительные матермалы, конструкции и сооружения, Вып. 5.- Тула: Изд-во ТулГУ, 2003. – С. 17-27.
- Баженов, Ю.М. Разработка теоретических основ проектирования железобетонных конструкций с учетом их экологической защищенности [Текст]/ Ю.М.Баженов, П.И.Новичков // Вестник отделения архитектуры и строительных наук. Вып.13, т.1 – Москва – Орел: РААСН, АСИ Орел ГТУ, 2009. – С. 28-36.