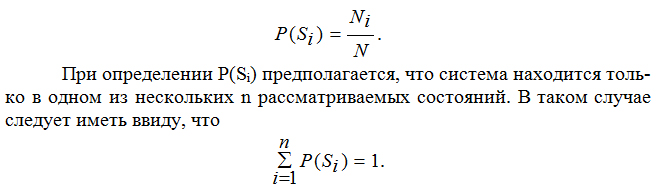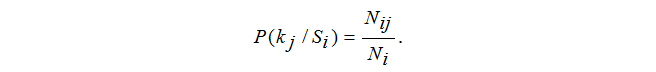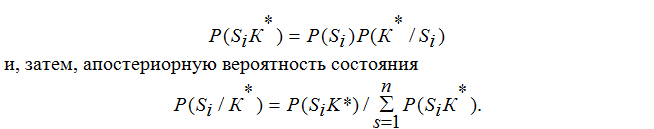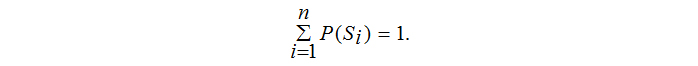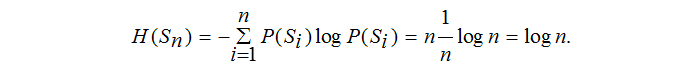ОПРЕДЕЛЕНИЕ КАТЕГОРИЙ ТЕХНИЧЕСКОГО СОСТОЯНИЯ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ ЗДАНИЙ И СООРУЖЕНИЙ С ИСПОЛЬЗОВАНИЕМ ВЕРОЯТНОСТНЫХ МЕТОДОВ РАСПОЗНАВАНИЯ

Соколов Владимир Алексеевич – Заведующий кафедрой «Строительные конструкции и материалы» Санкт-Петербургского государственного политехнического университета, кандидат технических наук, профессор

 

---

В литературных источниках справедливо отмечается, что область знаний и практической деятельности, называемая «обследование технического состояния зданий и сооружений» сложилась очень давно. Наряду с теоретическими исследованиями, проектной работой и строительством новых зданий и сооружений всегда осуществлялся анализ причин различных повреждений и разрушений существующих, уже давно эксплуатируемых объектов, а также проводились экспериментальные исследования и на моделях, и на натуре.

Вместе с тем, для такого практического и весьма специфичного рода деятельности конкретные и четкие рекомендации по принятию обоснованных решений о фактическом техническом состоянии находящегося в длительной эксплуатации строительного объекта, закрепленные в имеющихся нормативных документах, разработаны недостаточно. Важно подчеркнуть, что сказанное особенно актуально для специфики условий старой городской застройки исторического центра г.Санкт-Петербурга. Ведь именно здания старой городской застройки, в частности их строительная часть, в первую очередь нуждаются в проведении регулярных обследований технического состояния и грамотной организации этих работ.

В последние десять лет в этой области деятельности стали появляться весьма важные и полезные нормативные акты. Так, в 2003 году введен в действие Свод правил по проектированию и строительству СП 13–102–2003 «Правила обследования несущих строительных конструкций зданий и сооружений» [1]. Впервые нормативно закреплены основные термины, понятия и общие положения по ведению обследовательских работ, т.е. практически сняты многие существовавшие в литературе терминологические неточности и разночтения. Введено понятие и даны названия пяти категориям технического состояния и сформулированы определения по отнесению конструкций к каждой из них. В зависимости от присвоенной категории коротко изложены рекомендации по приведению конструкций в нормальное эксплуатационное состояние.

Нисколько не умаляя значимость этого документа, нельзя не отметить, что он нуждается в уточнении и совершенствовании. По существу его основные недостатки можно сформулировать следующим образом.

1. Видно, что введенные пять категорий технического состояния и по названиям, и по определениям взяты из накопленного опыта диагностики состояния бетонных и железобетонных конструкций, для которых многие диагностические признаки более-менее сформулированы. Требует доработки возможность применения этих же категорий при оценке технического состояния каменных, металлических и деревянных конструкций и, далее, к зданию в целом.
2. Присвоение той или иной категории по СП 13–102–2003 носит достаточно субъективный характер. Вместе с тем субъективизм снижается и даже сводится к минимуму, если назначению той или иной категории предшествуют накопленный опыт и имеющиеся статистические данные при оценке технического состояния многочисленных зданий подобного типа, т.е. опыт экспертов. Но эксперты используют накопленную статистику главным образом только в виде имеющейся по результатам обследования информации о многократном подтверждении правильности сделанных ранее оценок и правильности принятых проектных решений по устранению повреждений и, главное, в виде примеров их успешной реализации. То есть при назначении категорий состояния экспертами все равно принимаются волевые решения. Нет методик статистической обработки накопленной информации, а значит и каких-либо конкретных количественных критериев отнесения здания к той или иной категории состояния.

В 1997 году в Санкт-Петербурге вышли территориальные строительные нормы ТСН 50-302-96 «Устройство фундаментов гражданских зданий и сооружений в Санкт-Петербурге и на территориях, административно подчиненных Санкт-Петербургу» [2]. Затем, в 2004 году появился новый нормативный документ – ТСН 50-302-2004 «Санкт-Петербург. Проектирование фундаментов зданий и сооружений в Санкт-Петербурге» [3]. При этом, как указано в документе [3], он вводится взамен документа [2]. Сами по себе документы важны и очень нужны для обследовательской практики, однако в реальной практической деятельности возможно только их совместное, каким-то образом дозированное, существование, т.е. введение одного взамен другого только дезориентирует пользователей и привносит в реальную практику неразбериху. Если анализ подробностей такого «сосуществования» опустить, то в рамках рассматриваемой проблемы основные недостатки обоих документов можно сформулировать следующим образом.

1. И в том, и в другом документах также введены понятия категорий технического состояния зданий с различными конструктивными схемами. Но их всего три – первая, вторая и третья, и обозначены они римскими цифрами I, II и III. Признаки отнесения здания к той или иной категории весьма немногочисленны и ограничены, т.е. критерии сформулированы недостаточно четко. Таким образом, при назначении категорий по этим документам субъективизм проявляется в еще большей степени, чем по [1]. Более того, нет никакой связи между категориями по [1] и по [2, 3].
2. Вместе с тем, назначению категорий по [2, 3] придана очень большая практическая значимость, так как назначенная категория для обследуемого здания определяет вполне конкретные численные значения предельно допустимых дополнительных деформаций (осадок, перекосов и кренов), которые могут появиться при ведении любых работ как в самом здании при его реконструкции, так и вблизи него. Но эти данные, к сожалению, никак не увязаны с категориями по [1].

Для решения задач по определению достоверной картины технического состояния конструктивных элементов и здания в целом, а также для приведения существующей в обследовательской деятельности нормативной литературы в современный и согласованный вид предлагается использовать теоретический аппарат технической диагностики, основанный на вероятностных методах распознавания.

В [4] указано, что техническая диагностика – это научная дисциплина, которая занимается распознаванием состояний сложных технических систем, причем нередко в условиях ограниченной информации. Теоретическим фундаментом для решения задач технической диагностики следует считать общую теорию распознавания образов. Эта теория, составляющая важный раздел технической кибернетики, занимается распознаванием образов любой природы (геометрических, звуковых и т.п.), машинным распознаванием речи, печатного и рукописного текстов и т.д. Теоретический аппарат технической диагностики в настоящее время достаточно хорошо разработан в машиностроении, радиоэлектронике, радиолокации, компьютерной технике и в других отраслях, где используются технические системы с большим количеством повторяющихся элементов и большим объемом имеющейся статистической информации об их работе.

Применение аппарата и методов технической диагностики к таким сложным и зачастую уникальным техническим системам, как здание или сооружение (далее здание), является важным направлением не только в диагностировании состояний строительных конструкций и строительного объекта в целом, но и в создании для этого научно обоснованной нормативной базы. Научно обоснованное присвоение той или иной категории технического состояния здания является важным еще и потому, что позволяет вовремя распознать состояние системы, вовремя в нее «вмешаться» желательно без прекращения эксплуатации и вовремя определить степень, затраты и глубину этого инженерного вмешательства. Таким образом, снижается или сводится к минимуму риск при эксплуатации объекта (планирование текущих и капитальных ремонтов), при его реконструкции (частичной или полной), а также при проведении любых сделок с недвижимостью (покупка, продажа, аренда).

Постановка задачи при вероятностных методах распознавания такова. Имеется система (конструктивный элемент, здание или сооружение в целом), которая находится в одном из случайных состояний S_i. Здесь вполне допустимо ориентироваться на те пять состояний, которые приведены в нормах [1] для конструкций, т.е. считать, что состояния сформулированы. Предполагается также, что сформулирована совокупность признаков, каждый из которых с определенной вероятностью характеризует состояние системы (конструкции). При этом выполнен анализ диагностической ценности и диагностического веса признаков, которые, как принято в технической диагностике, определяются методами теории информации, вносимой признаками в систему состояний. В итоге требуется построить решающее правило, с помощью которого предъявленная (диагностируемая) совокупность признаков была бы отнесена к одному из возможных состояний (диагнозов). При этом важно оценить достоверность принятого решения, а также степень риска ошибочного решения.

Важное место в решении задач распознавания состояний систем отводится статистическим методам. Главное их преимущество состоит в возможности одновременного учета признаков различной физической природы, так как они характеризуются безразмерными величинами – вероятностями их проявления при различных состояниях системы. Одним из основных статистических методов является метод, основанный на простой формуле Байеса.

Суть метода состоит в том, что, если имеются состояние S_i (диагноз S_i) и простой признак k_j, встречающийся в этом состоянии, то вероятность совместного появления событий (наличия у системы состояния S_i и признака k_j) в соответствии с понятиями теории вероятностей (условная вероятность, зависимость несовместных событий) определится следующим образом:

Как совершенно справедливо отмечено в [4], очень важно определить точный смысл всех входящих в эту формулу величин, особенно для строительных объектов.

1. P(S_i/k_j) – вероятность состояния S_i после того, как стало известно наличие у рассматриваемого объекта признака k_j (апостериорная вероятность состояния). В данном случае это и есть искомый результат
2. P(S_i) – вероятность состояния S_i, определяемая по статистическим данным (так называемая априорная вероятность состояния). Так, если к моменту диагностирования предварительно обследовано N объектов и у N_i объектов оказалось состояние S_i, то

Применительно к зданиям и к упомянутым выше пяти категориям их технического состояния, которые можно положить в основу диагностирования, важно определить сколько же объектов нужно обследовать предварительно, причем так, чтобы результат с достаточной степенью точности можно было считать достоверным, т.е. чтобы выборка объектов из их генеральной совокупности (теоретически бесконечной) была бы вполне представительной (или, говорят, репрезентативной), позволяющей выполнить необходимую статистическую обработку.

3. P(k_j/S_i) – вероятность появления признака k_j у объектов с состоянием S_i. Если среди N_i объектов, имеющих состояние S_i, у части объектов N_ij проявился признак k_j, то тогда

4. P(k_j) – вероятность появления признака k_j у всех объектов независимо от состояния объекта. Пусть из общего числа N объектов признак k_j был обнаружен у N_j объектов. Тогда

В практических задачах диагностирование состояния зданий всегда проводится по комплексу признаков К, включающему множество признаков k₁ , k₂, …, k_t. У каждого из них вполне может быть несколько m разрядов с конкретными численными значениями (k_j1, k_j2, …, k_js, …, k_jm). В результате обследования устанавливается наличие у конструктивного элемента здания того или иного признака с соответствующим разрядом, т.е. говорят, что реализация у системы данного признака k_j^* становится известной и считается известной реализация всего комплекса признаков К^*. Тогда справедливо равенство 

Здесь и далее индекс ^* означает конкретное значение (реализация) признака.

В случае, когда обследование проводится по комплексу признаков, формула Байеса имеет вид

где P(S_i/К*) – вероятность диагноза S_i после того, как стали известны результаты обследования по комплексу признаков К.

Удобнее пользоваться обобщенной формулой Байеса, которая может быть записана так:

Вывод этой формулы здесь не приводится, с ним можно ознакомиться в [4]. Не вдаваясь в подробности вывода следует отметить, что знаменатель формулы Байеса для всех состояний одинаков. Это позволяет сначала определить вероятности совместного появления i-го состояния и данной реализации комплекса признаков

Для определения вероятности состояний по методу Байеса составляется так называемая диагностическая матрица. Эта матрица формируется в виде таблицы вероятностей признаков и их разрядов при различных диагнозах. Таким образом, таблица строится на основе предварительного статистического материала, т.е. в нее включены априорные вероятности состояний и признаков. После проведения серии расчетов по вышеуказанным зависимостям получается ряд апостериорных вероятностей каждого диагностируемого состояния либо по всей совокупности признаков и их разрядов, либо по части из них. Решающее правило, в соответствии с которым принимается решение о конкретном диагнозе, состоит в том, что объект с комплексом признаков К^* относится к состоянию S_i, если апостериорная вероятность этого состояния S_i является наибольшей, т.е.

К^*Є S_i, если P(S_i/К^*) > P(S _j/К^*) (j = 1, 2, …, n; i ≠ j).

Символ Є, применяемый в функциональном анализе, означает принадлежность множеству. Представленное выше условие указывает, что объект обладает данной реализацией комплекса признаков К^* или, короче, реализация К^* принадлежит состоянию (диагнозу) S_i.

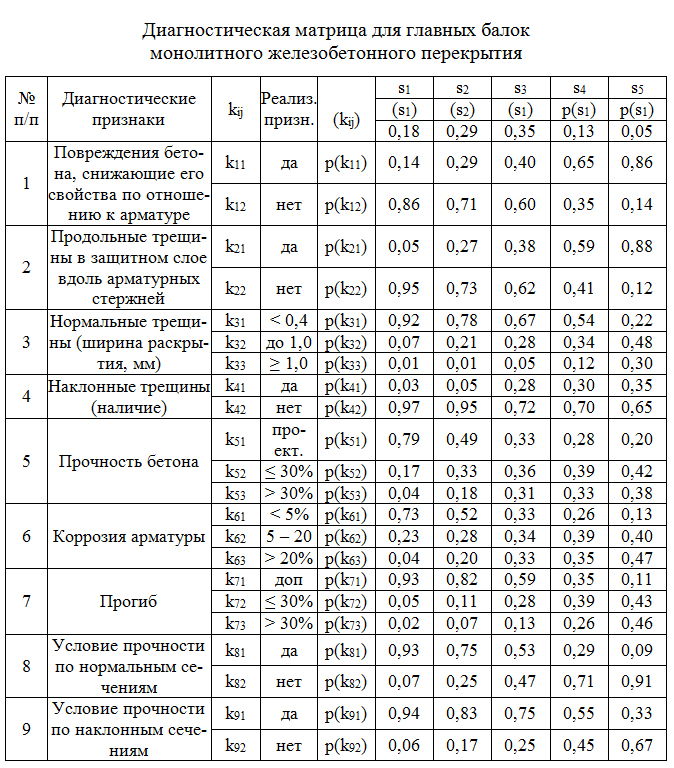
Сказанное выше иллюстрируется примером диагностирования состояний железобетонной балки, являющейся главной балкой монолитного железобетонного междуэтажного перекрытия промышленного здания старой городской застройки. Такие перекрытия состоят, как известно, еще из второстепенных балок, плитных участков и колонн, как элементов единой связанной системы. К моменту диагностирования обработана статистическая информация по ранее выполненным обследованиям подобных перекрытий. Пример статистической обработки приведен для ста главных балок, по результатам которой для этих балок построена диагностическая матрица (см. таблицу).

В таблицу включены априорные вероятности по пяти состояниям [1]: 1 – исправное, 2 – работоспособное, 3 – ограниченно работоспособное, 4 – недопустимое и 5 – аварийное. Диагностирование осуществляется по девяти признакам:

1) повреждения бетона, снижающие его защитные свойства по отношению к арматуре (следы коррозии, повреждения поверхности в виде сколов и отслоений); признак вводится как простой, т.е. диагностируется наличие этих повреждений («да») или их отсутствие («нет»);

2) продольные трещины в защитном слое бетона вдоль арматурных стержней, продукты коррозии вдоль арматурных стержней, отслоение защитного слоя бетона; признак также диагностируется по принципу «да» или «нет»;

3) наличие и ширина раскрытия нормальных трещин, которая определяется по результатам выполненных в ходе обследования измерений; вводится как трехразрядный признак; разделяется на величину менее 0,4 мм, на величину от 0,4 до 1 мм и на величину более 1 мм;

4) наличие наклонных трещин представляется как простой признак, свидетельствующий о наличии наклонных трещин («да») или об их отсутствии («нет»).

5) прочность бетона вводится как трехразрядный признак; определяется по результатам выполненных в ходе обследования измерений различными способами; разделяется на проектную прочность, на сниженную не более, чем на 30%, и на сниженную более, чем на 30%;

6) коррозия арматуры также рассматривается как трехразрядный признак; разделяется на степень поражения обнажившихся арматурных стержней не более, чем на 5%, далее 5–20% и затем более 20%;

7) прогиб определялся по результатам измерений и введен как трехразрядный признак, разделяющийся на допускаемый, превышающий допускаемый не более, чем на 30% и превышающий допускаемый более, чем на 30%;

8) проверка условия прочности по нормальным сечениям на основе результатов выполненной серии поверочных расчетов; признак вводится как простой, т.е. диагностируется выполнение условия («да») или его невыполнение («нет»);

9) проверка условия прочности по наклонным сечениям – вводится аналогично.

Как видно, для рассмотренных пяти состояний, в таблицу сведены априорные вероятности реализации указанных признаков в каждом состоянии, полученные на основе статистической обработки результатов ранее выполненных обследований упомянутых ста балок.

Далее, в ходе обследования следующей (например, сто первой) железобетонной балки указанные выше признаки проявились следующим образом:

1)   повреждения наружной поверхности есть;

2)   продольные трещины в защитном слое есть;

3)   нормальные трещины в растянутой зоне раскрытием до 0,4 мм есть;

4)   наклонные трещины есть;

5)   прочность бетона оказалась на 10% ниже проектной;

6)   имеет место обнажившаяся арматура, 5% сечения которой поражено коррозией;

7)   прогиб не превышает нормативный;

8)   условие прочности при расчете по нормальным сечениям удовлетворяется;

9)   условие прочности при расчете по наклонным сечениям удовлетворяется.

При использовании данных таблицы 1, предложенной выше методики и указанных условий получено следующее.

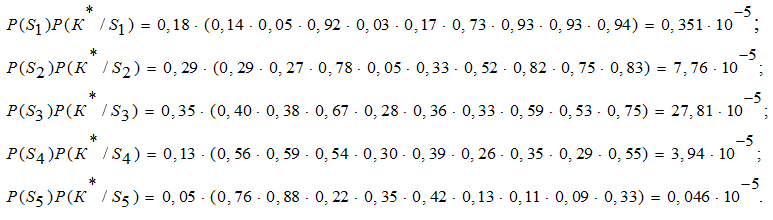
Как отмечено выше, знаменатель обобщенной формулы Байеса для всех состояний одинаков и определится по зависимости

Учитывая сформулированное выше решающее правило, диагностируемая балка по всей совокупности указанных диагностических признаков с вероятностью 0,697 может быть отнесена к третьей (ограниченно работоспособной) категории технического состояния.

Вместе с тем, анализируя полученные результаты (полученную информацию), можно отметить, что вероятность отнесения рассматриваемой балки к третьей категории не так высока. С какой степенью уверенности (вероятности) можно применить здесь указанное выше решающее правило и отнести состояние балки именно к третьей категории? Каков критерий отнесения, а точнее есть ли пороговое значение для вероятности диагноза P(S_i/K*). В [4] предлагается пороговый уровень распознавания принимать равным P(S_i/K*)>P_i, где P_i=0,9. Указано, что если P(S_i/K*)<P_i, то решение о диагнозе не принимается (отказ от распознавания) и в таком случае требуется поступление дополнительной информации.

В данном случае диагностирование состояний рассматриваемой балки при различных, реальных значениях априорных вероятностей (т.е. при реальных значениях диагностической матрицы) и при реальных результатах обследования, причем без возможности получить дополнительную информацию, привело к тому, что ни разу не удовлетворилось требование P(S_i/K*)>0,9. Вместе с тем, на основе многовариантного тестового расчета по указанной выше методике это требование удалось удовлетворить, но лишь при тех условиях, когда предлагаемый аппарат и не нужен, т.е. когда диагноз и так очевиден и однозначен.

Для оценки степени уверенности (вероятности) назначения указанной категории анализ полученных значений P(S_i/K*) предлагается выполнить с использованием методов теории информации.

В литературных источниках [4-6] отмечается, что теория информации возникла как математическая теория связи и, далее, получила применение в разных областях науки как общая теория связи статистических систем. В диагностике такими системами являются система состояний S_i (диагнозов) и связанная с ней система диагностических признаков К^*. Центральное место в теории информации занимает понятие энтропии системы. Энтропия в теории информации характеризует степень неопределенности системы.

Пусть рассматривается элемент технической системы S (балка), который может иметь несколько случайных состояний S_i с вероятностями P(S_i). Если одно из его состояний обязательно реализуется, а два состояния одновременно невозможны (в теории вероятностей – это полная группа несовместных событий), то

Именно таким, как отмечено выше, является рассматриваемый элемент системы (балка) и именно такие системы в рамках теории информации рассматриваются далее.

В теории информации энтропия системы, имеющей n возможных состояний с вероятностями P(S₁), P(S₂), …, P(S_n), определяется зависимостью

В работах [5,6] показано, что при выполнении некоторых достаточно общих требований (непрерывности, неубывания энтропии при возрастании числа состояний, аддитивности) указанное определение энтропии является единственным. Так как вероятности состояний любой системы 0≤P(S_i)≤1, то энтропия представляет собой существенно положительную величину.

Вычислим энтропию системы, имеющей n состояний. Если они равновероятны, то

Как видно, энтропия системы с одинаковыми вероятностями состояний равна логарифму числа состояний. Очевидно, что с увеличением числа состояний энтропия возрастает, но гораздо медленнее, чем число состояний. В таком случае важное свойство энтропии состоит в следующем: если система имеет несколько состояний, то энтропия будет максимальной в том случае, когда все состояния равновероятны. В [4] приводится доказательство этому, из которого вытекает важная оценка энтропии произвольной системы

H(S)≤log n,

где n – число возможных состояний системы.

В данном случае при n=5 значение H(S)=log 5≈0,700. Чем ближе энтропия элемента системы к этому значению, тем больше неопределенность при распознавании его состояний. Чем она дальше, т.е. ближе к нулю, тем неопределенность ниже. В рассматриваемом примере энтропия H(S_n) состояния рассматриваемого элемента системы – балки, получилась равной

Далее вводится понятие степени определенности рассматриваемого элемента системы в соответствии с зависимостью

V(S_n) = H(S) — H(S_n) = 0,700 – 0,358 = 0,342.

Таким образом, обследуемый элемент системы – главная балка монолитного железобетонного перекрытия с вероятностью 0,697 относится к третьей (ограниченно работоспособной) категории технического состояния с относительной степенью определенности этого состояния, равной 0,342/0,700=0,490. Эти параметры в дальнейшем используются при анализе технического состояния и степени его определенности уже для более сложной системы – перекрытия в целом, состоящего из указанных выше отдельных элементов-систем. Так, основываясь на терминологии теории информации, параметр V(S_n) представляет не что иное как количество внесенной информации о состоянии S_n относительно состояния S, имеющего максимальную степень неопределенности. Его далее предлагается рассматривать как вклад состояния данного элемента системы в состояние перекрытия в целом.

 

Библиографический список

 

1. СП 13-102-2003. Правила обследования несущих строительных конструкций зданий и сооружений. Свод правил по проектированию и строительству. Госстрой России. ГУЛ ЦПП. 2003.
2. ТСН 50-302-96. Устройство фундаментов гражданских зданий и сооружений в Санкт-Петербурге и на территориях, административно подчиненных Санкт-Петербургу. – СПб., 1997.
3. ТСН 50-302-2004. Санкт-Петербург. Проектирование фундаментов зданий и сооружений в Санкт-Петербурге. – СПб., 2004.
4. Биргер И.А. Техническая диагностика. – М.: Машиностроение, 1978. – 240 с., ил. – (Надежность и качество).
5. Файнстейн А. Основы теории информации. – М.: Изд-во иностранной литературы, 1965.
6. Шеннон К. Работы по теории информации и кибернетики. – М.: Изд-во иностранной литературы, 1963.