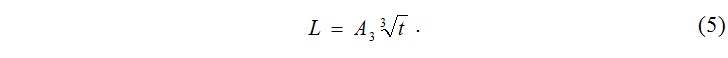Латыпов Валерий Марказович – Заведующий кафедрой «Строительные конструкции» ГОУ ВПО «УГНТУ», доктор технических наук, профессор, член-корреспондент РАЕН
Анваров Аскар Рамилевич – Ассистент кафедры «Строительные конструкции» ГОУ ВПО «УГНТУ», кандидат технических наук
Латыпова Татьяна Владимировна – Доцент кафедры «Водоснабжение и водоотведение» ГОУ «ВПО УГНТУ», кандидат технических наук
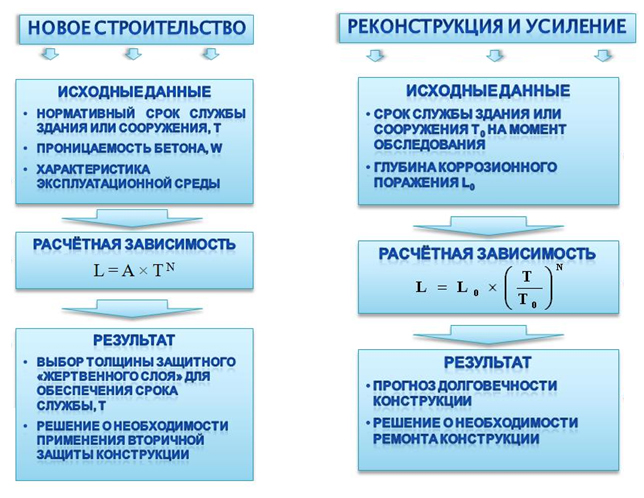
В связи с интенсивным развитием в нашей стране монолитного строительства здании повышенной этажности одной из важнейших задач на стадии проектирования является оценка надёжности конструкций в соответствии с требованием ГОСТ Р22.1.12-05 «Национальный стандарт Российской Федерации. Безопасность в чрезвычайных ситуациях». Одним из элементов надежности является долговечность. Для выполнения оценки долговечности необходимо иметь нормативную методику расчёта долговечности железобетона, которая согласно СНиП 2.03.11-85 «Защита строительных конструкций от коррозии» может быть обеспечена с использованием средств первичной и вторичной защиты. Согласно СНиП 2.03.11-85 «Защита строительных конструкций от коррозии» [8] расчётная долговечность может быть обеспечена средствами первичной и вторичной защиты. Первичная защита – это повышение плотности бетона и толщины защитного слоя, вторичная – это нанесение разного рода покрытий и пропиток. Однако средства вторичной защиты имеют два недостатка: высокая стоимость (в средне- и сильноагрессивной среде в несколько раз превышающая стоимость самой конструкции), вторичная защита недолговечна и требует возобновления через каждые 5-10 лет. Особенностью монолитных зданий с каркасом является то, что большая часть железобетонных конструкций остаётся в структуре многослойных стен и является недоступной для возобновления средств вторичной защиты. То есть для обеспечения долговечности конструкций фактически можно рассчитывать лишь на средства первичной защиты. В связи с этим расчётное обоснование параметров защитного слоя бетона (его толщины и плотности), гарантирующих обеспечить защиту арматуры от коррозии на весь срок эксплуатации конструкции, удовлетворив при этом требованиям рентабельности капиталовложений, является до настоящего времени актуальной, однако, не решенной задачей.
Долговечность железобетона при коррозионном воздействии внешней среды можно условно разделить на два периода (рис.1):
Т = t1 + t2. (1)
Однако, фактически в качестве долговечности Т целесообразно рассматривать только срок t1 (до начала коррозии арматуры), то есть пренебрегая сроком t2, поскольку погрешность в определении срока t2 может быть очень большой. Именно такой подход используется большинством исследователей [1, 2, 4, 5], хотя попытки более или менее достоверного определения срока t2 уже предпринимаются [7]. До настоящего времени не существует нормативных расчётных методов определения срока t1, что определяет актуальность исследований в этой области. Действительно, зависимость глубины повреждения бетона от срока эксплуатации должна лежать в основе принятия решения как при проектировании новых объектов, так и при оценке ресурса эксплуатирующихся конструкций (рис.2). Поскольку существование железобетона возможно лишь при условии наличия защитного слоя аз и сцепления арматуры с бетоном, то наиболее удобно определять срок t1 по функциональной зависимости глубины поражения L=f(t), исходя из условия L < аз.
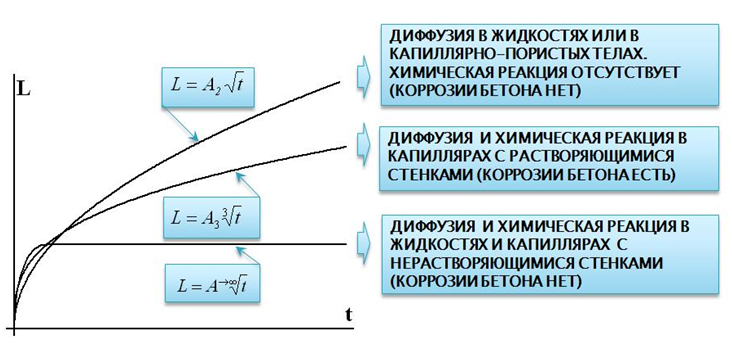
Очевидно, что конечной целью построения математической модели коррозии L=f(t) является получение простой формулы, по которой удобно выполнять инженерные расчеты. Коррозия бетона связана с взаимодействием полиминерального цементного камня с многокомпонентной внешней средой. Однако, практически все исследователи при выводе зависимости L=f(t) с целью упрощения исходят из взаимодействия только двух веществ. Математическая модель физико-химического взаимодействия двух веществ известна уже давно – это дифференциальные уравнения второго порядка в частных производных, в которых одновременно учитываются диффузия, растворение и химическое взаимодействие двух компонентов А (внешняя среда) и В (в случае коррозии бетона – это растворимые компоненты цементного камня) со скоростью реакции «медленной» или «быстрой» (рис.3; табл.1, уравнение (2)).
Для более простых случаев («мгновенная» реакция или «реакция не протекает») процесс определяется только диффузией (рис.3; табл.1, уравнение (3)).
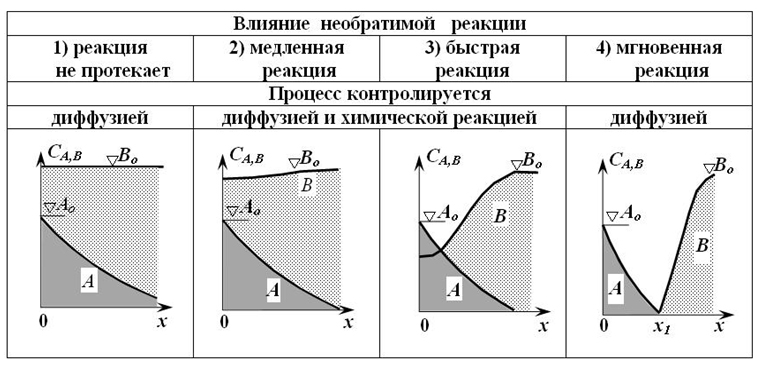
Рис. 3. Типы кривых, характеризующих распределение концентрации при бимолекулярной реакции вида: А + В продукты согласно исследованиям Т. Шервуда, Р. Пигфорда, Ч. Уилки [9]. Примечание: х = х1 – координата реакционной плоскости
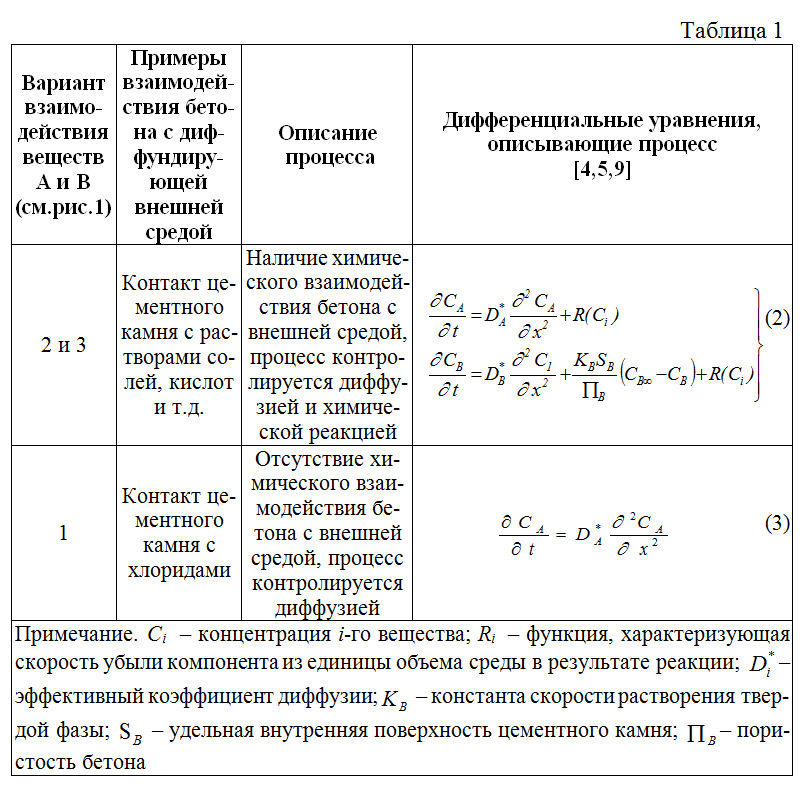
До последнего времени «камнем преткновения» всех моделей было получение простой инженерной формулы из системы уравнений (2). Дело в том, что математически система уравнений типа (2) не имеет аналитического решения. Поэтому большинство исследователей «упрощали» уравнение, приравнивая Ri(c) ~ 0, и, таким образом, фактически переходили к уравнению (3), известному также как второй закон Фика. В то же время, уравнение (3) имеет аналитическое решение в виде общепринятого в области долговечности железобетона «закона корня квадратного от времени»:
где L – глубина нейтрализации бетона, мм;
t – срок эксплуатации, г;
A – коэффициент, зависящий от концентрации углекислого газа C, эффективного коэффициента диффузии D¢ и реакционной емкости бетона m0.
Разработанные на основе этих принципов отечественными и зарубежными исследователями (С.Н. Алексеев, В.Г. Батраков, Е.А. Гузеев, Б.В. Гусев, Т.К. Дементьев, Ф.М. Иванов, В.М. Москвин, А.Ф. Полак, Ш.М. Рахимбаев, В.Б. Ратинов, Н.К. Розенталь, В.Ф. Степанова, А.С. Файвусович, В.В. Яковлев, а также K. Kishitany, T. Nishi, H.G. Smolzyk, M. Hamada, H.I. Wiering) математические модели сводятся, в конечном счете, к выражению вида (4).
В нашей стране наиболее весомый вклад в развитие расчётных методов обеспечения долговечности железобетона внёс профессор А.Ф. Полак в 70-80 гг. XX века путём применения метода «квазистационарного» режима и разделения корродирующего слоя на зоны. Несмотря на то, что полученная проф. А.Ф. Полаком формула для определения глубины проникания внешней среды вглубь цементного камня учитывала большое количество параметров процесса, она по прежнему являлась одной из разновидностей «закона корня квадратного от времени». Математическая модель вида (4) основана на решении дифференциальных уравнений, описывающих различные физические и химические процессы коррозии. Однако, эти решения были получены на основе ряда принятых допущений, что могло привести к снижению точности результатов. Одним из неучтённых в модели (4) процессов является наличие химического взаимодействия внешней среды с растворимыми компонентами цементного камня, которое приводит к снижению скорости проникновения агрессивной среды в бетон. Учёт этого процесса может существенно повлиять на вид получаемой расчётной зависимости L=f(t) (рис.4).
Развитие и уточнение существующей инженерной формулы вида (4) было произведено путём проведения вычислительного эксперимента с использованием компьютерной системы символьной (аналитической) математики Maple 9.5, а именно – построение математической модели, основанной на численном решении системы дифференциальных уравнений, объединяющей большее количество параметров процесса. Результаты численного эксперимента позволяют сделать вывод о том, что при наличии выраженного химического взаимодействия внешней среды с растворимыми компонентами цементного камня математической моделью коррозии бетона является выражение
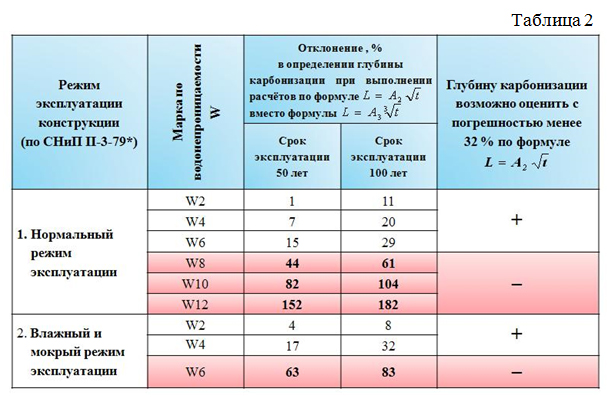
Полученные данные (табл.2) подтверждают применимость зависимости вида для бетонов высокой проницаемости с относительно небольшим проектным либо фактическим сроком эксплуатации. Проектирование же долговечности конструкций из бетонов марок W6 и выше на длительные сроки эксплуатации целесообразно осуществлять с использованием зависимости (рис.4).
На основе данных обследования технического состояния бетонных и железобетонных конструкций, проведенных на нескольких сотнях объектов с разным режимом эксплуатации, определёны значения A3 (см. табл.3) в зависимости от плотности бетона и температурно-влажностного режима эксплуатации конструкции, когда коррозия бетона протекает в так называемых «обычных условиях» эксплуатации, а причиной коррозии арматуры является карбонизация защитного слоя бетона.
Таким образом, на этапе проектирования конструкций достижение нормативного срока эксплуатации в обычных условиях эксплуатации (то есть при воздействии углекислого газа воздуха и влаги) возможно обеспечить средствами только первичной защиты – назначением толщины защитного слоя aз, а также марки бетона по водонепроницаемости W (рис.5). Например, при толщине защитного слоя aз = 30 мм нормативный срок эксплуатации Тн=100 лет может быть обеспечен при использовании обычного бетона с маркой по водонепроницаемости W4, если же aз=15 мм, то нормативный срок Тн=100 лет может быть достигнут без применения средств вторичной защиты только при использовании бетона особо низкой непроницаемости с маркой не ниже W8.
В настоящее время на предприятиях стройиндустрии есть все необходимое для обеспечения необходимой марки бетона по водонепроницаемости и жесткого контроля за толщиной защитного слоя бетона, что позволяет инвесторам, заказчикам, проектировщикам и строителям быть уверенными в возможности реализации проектных решений по достижению планируемой долговечности.

Рис. 5. Зависимость срока эксплуатации конструкции T от марки по водонепроницаемости W в нормальных условиях эксплуатации при значениях толщины защитного слоя бетона: 1 – aз = 30 мм; 2 – aз = 25 мм; 3 – aз = 20 мм; 4 – aз = 15 мм
Библиографический список
- Алексеев, С.Н. Долговечность железобетона в агрессивных средах / С.Н. Алексеев, Ф.М. Иванов, C. Модры, П. Шиссль. – М.: Стройиздат, 1990. 320 с.
- Алексеев, С.Н. Коррозионная стойкость железобетонных конструкций в агрессивной промышленной среде / С.Н. Алексеев, Н.К. Розенталь. – М.: Стройиздат, 1976. 205 с.
- Анваров, А.Р. Обоснование достаточности средств первичной защиты для достижения проектной долговечности железобетона в естественных условиях эксплуатации: автореф. дис. … канд. тех. наук / А.Р. Анваров. – Уфа: УГНТУ, 2007. 22 с.
- Гусев, Б.В. Математические модели процессов коррозии бетона / Б.В. Гусев, А.С. Файвусович, В.Ф. Степанова и др. – М.: ИИЦ «ТИМР», 1996. 103 с.
- Полак, А.Ф. Моделирование коррозии железобетона и прогнозирование его долговечности / А.Ф. Полак // Итоги науки и техники. Коррозия и защита от коррозии. Т.XI. – М.: ВИНИТИ, 1986. С. 136–180.
- Полянин, А. Д. Справочник по линейным уравнениям математической физики / А.Д. Полянин. – М.: Физматлит, 2001. 576 с.
- Прокопович, А.А. Сопротивление изгибу железобетонных конструкций с различными условиями сцепления продольной арматуры с бетоном / А.А. Прокопович. – Самара: НВФ «Сенсоры. Модули. Системы», 2000. 296 с.
- СНиП 2.03.11‑85. Защита строительных конструкций от коррозии. – М.: ЦИТП Госстроя СССР, 1986. 46 с.
- Шервуд Т. Массопередача / Пигфорд Р., Уилки Ч. (пер. с англ.). – М.: Химия, 1982. 96 с.
- Tetsuya Ishida/ Theoretically Identified Strong Coupling of Carbonation Rate and Thermodynamic Moisture States in Micropores of Concrete/ Koichi Maekawa? Masoud Soltani – Journal of Advanced Concrete Technology Vol. 2, No. 2, 213-222, June 2004.