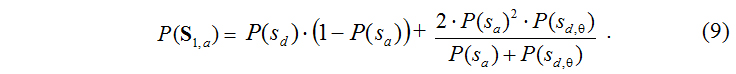Стефанишин Дмитрий Владимирович – Ведущий научный сотрудник
Института телекоммуникаций и глобального информационного
пространства Национальной академии наук Украины, г.Киев,
доктор технических наук
Романчук Екатерина Геннадиевна – Аспирантка Института
телекоммуникаций и глобального информационного пространства
Национальной академии наук Украины, г.Киев
За последнее десятилетие на объектах гидроэнергетики произошло несколько аварий, которые можно назвать нетиповыми, поскольку раньше подобные аварии в мировой практике еще не случались [1-6]. Ход этих аварий сопровождался отказами автоматических средств контроля и регулирования, оснащенных современной компьютерной техникой.
Одна из таких аварий произошла 14 декабря 2005 г. на ГАЭС Таум Саук (Taum Sauk, штат Миссури, США). В результате аварии разрушилась дамба ограждения верхового бассейна ГАЭС (рис. 1).
По результатам расследования аварии было установлено, что причинами разрушения дамбы ограждения верхового бассейна ГАЭС Taum Sauk были его переполнение и перелив воды через гребень дамбы вследствие сбоя в компьютерной программе системы автоматического регулирования уровня воды в бассейне [1, 2].
Другая авария произошла 17 августа 2009 года на Саяно-Шушенской ГЭС (Россия, Хакассия) в результате разгерметизации напорного тракта и разрушения одного из гидроагрегатов (рис. 2).
Авария получила катастрофическое развитие вследствие отказа автоматики, которая не сработала в режиме перекрытия напорного тракта аварийно-ремонтным затвором. При аварии погибло 75 работников ГЭС [3, 4].
В обоих случаях аварии носили сложный системный характер с вовлечением в механизмы их возникновения и развития отказов автоматических средств обеспечения безопасности объектов.
С целью установления роли автоматических средств контроля и регулирования в ходе аварий на ГАЭС Taum Sauk (2005 г.) и на Саяно-Шушенской ГЭС (2009 г.) авторами было осуществлено вероятностное моделирование гипотетических сценариев развития аварий с учетом отказов систем автоматики и произведены расчеты вероятностей аварий при разных значениях вероятностей отказов автоматических устройств.
При моделировании и оценке вероятности аварии на ГАЭС Taum Sauk рассматривались система S1,а ={sd, sa} в составе оградительной дамбы верхового бассейна (подсистема sd) и системы автоматического регулирования уровня воды в бассейне (подсистема sa).
Принимались следующие обозначения для вероятностей аварийных событий: Р(sd) – вероятность разрушения дамбы по независимым от работы автоматики причинам (вероятность отказа подсистемы sd); Р(sa) – вероятность отказа системы автоматического регулирования уровня (вероятность отказа подсистемы sa).
Авария на верховом бассейне ГАЭС Taum Sauk могла бы и не состояться, если бы в оригинальном проекте на случай отказа автоматики был предусмотрен аварийный водослив. Работоспособность аварийного водослива в системе при отказе подсистемы автоматического регулирования моделировалась условием Ɵ. Вероятность разрушения дамбы при этом условии обозначена как Р(sd,Ɵ).
Для того чтобы состоялось событие (S1,а,Ɵ), должны произойти два отказа: сначала подсистемы sa, затем подсистемы sd. Пусть Р(sa)* – безусловная вероятность появления отказа подсистемы sa при условии, что отказ подсистемы sd не произойдет раньше, чем откажет sa. Тогда [7] полная вероятность аварийного события (S1,а,Ɵ):
В соответствии с теоремой Байеса для полной группы событий
В результате, с учетом (1), (2), (8) получаем полную вероятность возникновения аварии в системе S1,а:
На рис. 3 приводятся результаты имитационного моделирования вероятности возникновения аварии в системе S1,а в зависимости от изменения вероятности отказа подсистемы sa (системы автоматического регулирования уровня воды в верховом бассейне ГАЭС). Моделирование осуществлялось при различных значениях вероятности разрушения дамбы верхового бассейна вследствие независимых от работы автоматики причин (отказа подсистемы sd) Р(sd) при условии, что в случае отказа подсистемы sa вероятность разрушения дамбы Р(sd,Ɵ)= 1.
В частности, при исследованиях были промоделированы шесть случаев, когда:
1) Р(sd)= 5×10–3, год–1;
2) Р(sd)= 10–3, год–1;
3) Р(sd)= 5×10–4, год–1 (допускаемая действующими нормами [9] вероятность аварии на напорных гидросооружениях II класса);
4) Р(sd)= 10–4, год–1;
5) Р(sd)= 5×10–5, год–1 (нормативная вероятность аварии [9] на напорных гидросооружениях I класса);
6) Р(sd)= 10–5, год–1.
Анализируя графики на рис. 3, можно заметить, что во всех модельных случаях, когда вероятность отказа для системы автоматического регулирования уровня воды в верхнем бассейне ГАЭС начинает превышать некоторое «пороговое» значение, вероятность аварии в системе S1,а начинает стремительно возрастать уже при незначительном увеличении вероятности отказа автоматики. При принятых нами вероятностях Р(sd) это «пороговое» значение вероятности отказа системы автоматического регулирования меняется в пределах 10–3¸4×10–2, год–1. При этом при превышении «порога» для Р(sa) вероятность Р(S1,a) практически перестает зависеть от вероятности первичного (независимого) отказа подсистемы sd (т.е. собственно от надежности дамбы) и начинает зависеть главным образом от надежности автоматики.
На рис. 4 приводятся результаты имитационного моделирования вероятности системной аварии Р(S1,a) в зависимости от изменения вероятности отказа подсистемы sa при постоянном значении вероятности первичного отказа подсистемы sd (вероятность Р(sd)= 10–3, год–1) и при различных значениях вероятности Р(sd,Ɵ):
1) Р(sd,Ɵ) = 1;
2) Р(sd,Ɵ) = 10–1, год–1;
3) Р(sd,Ɵ) = 10–2, год–1;
4) Р(sd,Ɵ) = 10–3, год–1;
5) Р(sd,Ɵ) = 5×10–4, год–1;
6) Р(sd,Ɵ) = 10–4, год–1.
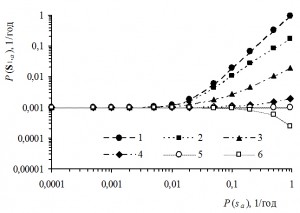
Рис. 4. Графики зависимости вероятности аварии в системе S1,a от вероятности отказа подсистемы sa при Р(sd)= 10–3, год–1
Анализируя графики на рис. 4, можно заметить, что при снижении вероятности разрушения дамбы Р(sd,Ɵ) при отказе подсистемы автоматического регулирования за счет работы аварийного водослива влияние отказов автоматики на вероятность Р(S1,a) постепенно уменьшается.
При моделировании и оценке вероятности развития аварии на Саяно-Шушенской ГЭС рассматривалась система S2,a = {s1, a1,2, s2} в составе: агрегат ГЭС – основная подсистема (s1); аварийный затвор – подсистема (s2), пребывающая в «холодном» резерве; автоматический переключатель на резерв (a1,2). При этом предполагалось, что подсистема s2 должна «включаться» в работу автоматическим переключателем a1,2 в случае отказа основной подсистемы s1 и предупреждать дальнейшее развитие аварии.
Учитывались два возможные, несовместные, сценария развития аварии: сценарий A1 – при работоспособном автоматическом переключателе на резерв отказывают как основная s1, так и резервная s2 подсистемы; сценарий A2 – сначала отказывает автоматический переключатель на резерв a1,2, а затем отказывает s1 [10].
Несовместность сценариев A1 и A2 позволяет при оценке вероятности P(S2,a) развития аварии в системе S2,a воспользоваться формулой полной вероятности. Имеем:
P(S2,a) = P(A1)+P(A2), (10)
где P(A1), P(A2) – вероятности реализации сценариев A1 и A2 соответственно.
Вероятность P(A1) определим при условии, что автоматический переключатель a1,2 непосредственно при отказе подсистемы s1, которая резервируется, пребывает в работоспособном состоянии (обозначим это условие как Ɵ1); вероятность P(A2) – при условии, что a1,2 переходит в неработоспособное состояние еще при работоспособной подсистеме s1, которая резервируется (пусть это будет условие Ɵ2).
Условия Ɵ1, Ɵ2, по определению, формируют полную группу событий. Поскольку сумма вероятностей условий Ɵ1 и Ɵ2 должна равняться единице, то для того чтобы задать вероятности их реализации, достаточно определить, с какой вероятностью устройство a1,2 откажет при работоспособной подсистеме s1.
Для оценки вероятности отказа устройства a1,2 при условии, что подсистема s1 находится в работоспособном состоянии, выделим из состава системы S2,a некоторую условную систему Sir1,a, формируемую подсистемой s1 и автоматическим переключателем на резерв a1,2.
Предположим, что система Sir1,a (индекс обозначает «без резервирования») находится в работоспособном состоянии в случае, если подсистема s1 и автоматический переключатель на резерв a1,2 являются работоспособными, и отказывает, если откажет s1 либо a1,2. Пусть также между отказами подсистемы s1 и автоматического переключателя на резерв a1,2 отсутствуют стохастические связи, т.е. s1 и a1,2 отказывают вследствие собственных, независимых, внутренних, причин.
Тогда вероятность отказа устройства a1,2 при условии, что подсистема s1 находится в работоспособном состоянии, определится как вероятность отказа системы Sir1,a вследствие выхода из строя a1,2.
Сформируем полную группу событий, как и в случае системных отказов A1 и A2, и воспользуемся формулой полной вероятности. В результате получим:
Поскольку, по определению, для соответствующих событий-отказов справедливы отношения
Откуда после преобразований получим:
где Р(s1), Р(a1,2), Р(s2) – вероятности отказов подсистем s1, a1,2, s2 соответственно.
На рис. 5 приводятся графики зависимости вероятности развития аварии в системе S2,a от вероятности отказа автоматического переключателя на резерв a1,2 при различных значениях вероятности отказов подсистемы s1 (вероятностей разрушения гидроагрегата вследствие независимых от работы автоматики причин):
1 – Р(s1) = 10–1, год–1;
2 – Р(s1) = 5×10–2, год–1;
3 – Р(s1) = 10–2, год–1;
4 – Р(s1) = 5×10–3, год–1;
5 – Р(s1) = 10–3, год–1.
Вероятность Р(s2) отказа аварийно-ремонтного затвора (отказа подсистемы s2) принималась согласно статистическим данным [11]: Р(s2) = 10–2, год–1.
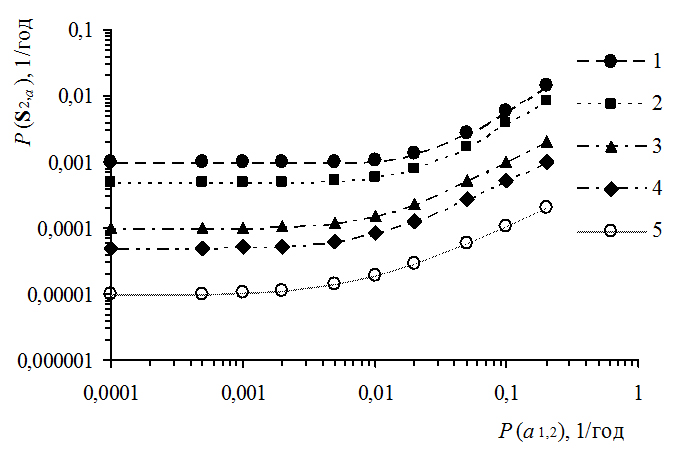
Рис. 5. Графики зависимости вероятности развития аварии в системе S2,a от вероятности отказа автоматического переключателя на резерв a1,2 при различных значениях вероятности разрушения гидроагрегата и Р(s2) = 10–2, год–1
Кроме того, дополнительно анализировалось влияние на вероятность развития аварии в системе S2,a работоспособности аварийно-ремонтного затвора (подсистемы s2).
На рис. 6 приводятся графики зависимости вероятности развития аварии в системе S2,a от вероятности отказа автоматического переключателя на резерв а1,2 при различных значениях вероятности отказа аварийно-ремонтного затвора (подсистемы s2):
1 – Р(s2) = 10–1, год–1;
2 – Р(s2) = 5×10–2, год–1;
3 – Р(s2) = 10–2, год–1;
4 – Р(s2) = 5×10–3, год–1;
5 – Р(s2) = 10–3, год–1.
Вероятность Р(s2) разрушения гидроагрегата вследствие независимых от автоматики причин (отказа подсистемы s1) принималась равной Р(s1)= 5×10–2, год—1. Эта вероятность определяет 95% надежность агрегата.
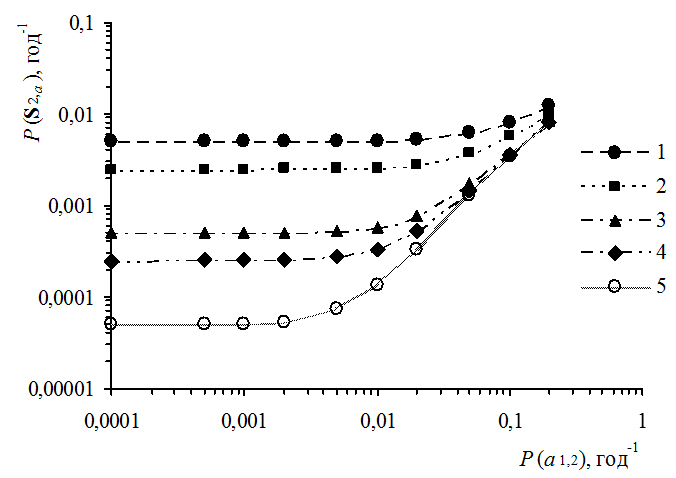
Рис. 6. Графики зависимости вероятности развития аварии в системе S2,a от вероятности отказа автоматического переключателя на резерв a1,2 при различных значениях вероятности отказа аварийно-ремонтного затвора и Р(s1) = 5×10-2, год-1
Можно заметить, что в обоих случаях (см.рис. 5, 6) имеет место рост вероятности развития аварии в системе S2,a при увеличении вероятности отказа автоматического переключателя на резерв a1,2 с превышением значений, близких к 10-2, год-1. При этом отмечается высокая чувствительность вероятности развития аварии в системе к отказам автоматики в условиях, когда для обеспечения безопасности большее внимание уделяется надежности резервной подсистемы, а не основной подсистемы.
По результатам проведенных исследований можно сделать обобщающий вывод о возможности негативного влияния недостаточно надежных средств автоматического регулирования, устанавливаемых на энергетических объектах, на аварийность объектов. В то же время при обеспечении высокой работоспособности автоматики, при вероятностях отказов 10-3 год-1 и ниже, можно минимизировать влияние автоматики на безопасность гидроэнергетического объекта.
Библиографический список
- http://www.ferc.gov/industries/hydropower/safety/projects/taum-sauk/staff-rpt.asp. Taum Sauk Pumped Storage Project (No. P-2277). Dam Breach Incident. Incident Description. FERC Staff Report, April 28, 2006.
- http://www.ferc.gov/industries/hydropower/safety/projects/taum-sauk/ipoc-rpt/full-rpt.pdf. Taum Sauk Pumped Storage Project (No. P-2277). Dam Breach Incident. Incident Description. ERC Independent Panel of Consultants (IPOC) Report, May 25, 2006.
- http://ru.wikisource.org/wiki/ Акт технического расследования причин аварии на Саяно-Шушенской ГЭС 17 августа 2009 года. Материал из Викитеки – свободной библиотеки.
- http://www.powermag.com/issues/features/Investigating-the-Sayano-Shushenskaya-Hydro-Power-Plant-Disaster_3229.html. Investigating the Sayano-Shushenskaya Hydro Power Plant Disaster// By A Boyko and S Popov, EKRA-Sibir Ltd. and Nemanja Krajisnik, Siemens Transmission and Distribution Ltd.
- Брызгалов В.И. Из опыта создания и освоения Красноярской и Саяно-Шушенской гидроэлектростанций. Красноярск: Сибирский изд. дом «Суриков», 1999. – 562 с.
- Гидротехническое строительство. НТФ «Энергопрогресс». Ежемесячный научно-технический журнал. №11. 2008.
- Стефанишин Д.В., Романчук К.Г. Про граничні оцінки ймовірностей техногенних аварій внаслідок малоймовірних сполучень навантажень// Problems of decision making under uncertainties. Abstracts of XVI Int. Yalta, Ukraine, October 4-8, 2010. P.P. 128-129.
- Стефанишин Д.В. Вибрані задачі оцінки ризику та прийняття рішень за умов стохастичної невизначеності. – К.: Азимут-Україна, 2009. – 104 с.
- СНиП 33-01-2003. Гидротехнические сооружения. Основные положения. –М.: Госстрой России, 2004.
- Стефанишин Д.В., Романчук К.Г. Оцінка ймовірності відмови зарезервованої системи з автоматичним перемиканням на резерв// Вісник НУВГП. Зб. наук. праць. Вип. 4 (44). Рівне: НУВГП. 2008. С. 334-340.
- Lagerholm S. Safety and reliability of spillway gates// Repair and upgrading of dams Symposium. -Stockholm: 1996. -P. P. 362-373.